In this publication, we will consider one of the classical theorems of affine geometry – the Ceva theorem, which received such a name in honor of the Italian engineer Giovanni Ceva. We will also analyze an example of solving the problem in order to consolidate the presented material.
Statement of the theorem
Triangle given ABC, in which each vertex is connected to a point on the opposite side.
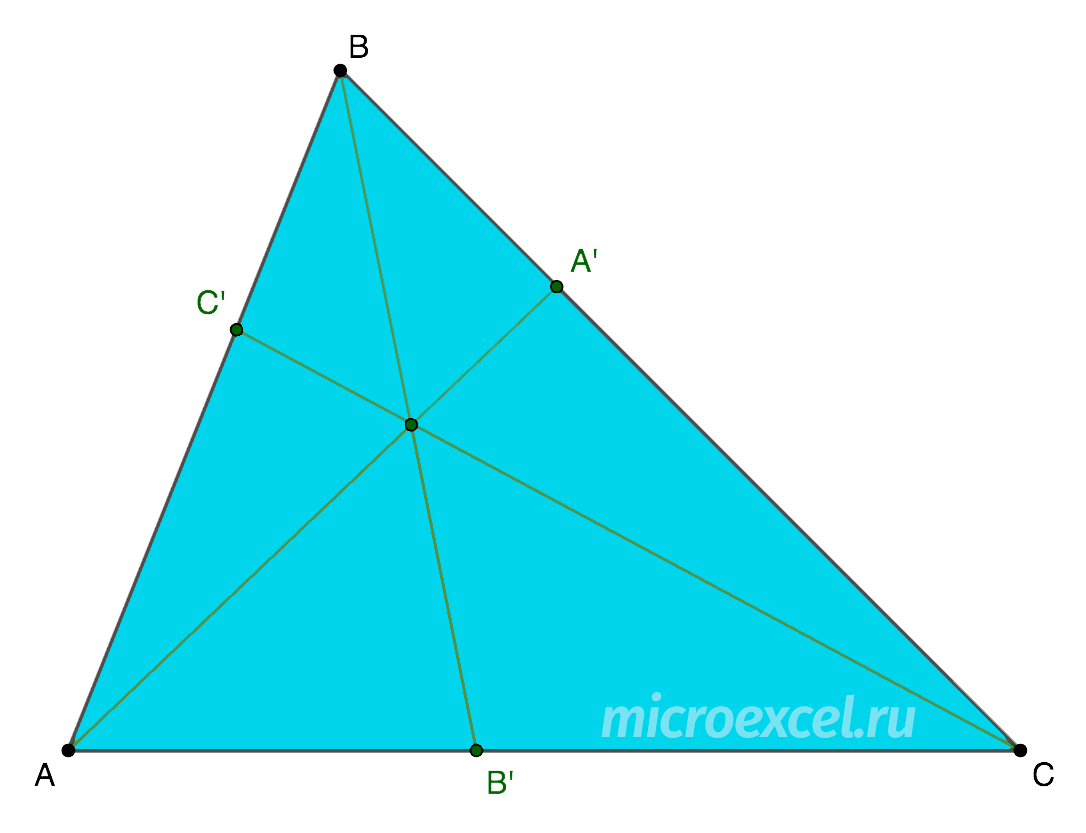
Thus, we get three segments (AA’, BB’ и CC’), which are called cevians.
These segments intersect at one point if and only if the following equality holds:
|AND’| |NOT’| |CB’| = |BC’| |SHIFT’| |AB’|
The theorem can also be presented in this form (it is determined in what ratio the points divide the sides):
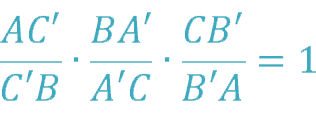
Ceva’s trigonometric theorem
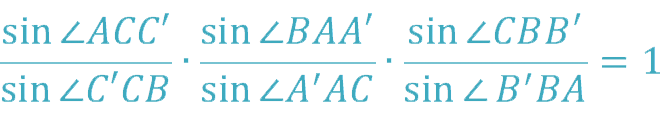
Note: all corners are oriented.
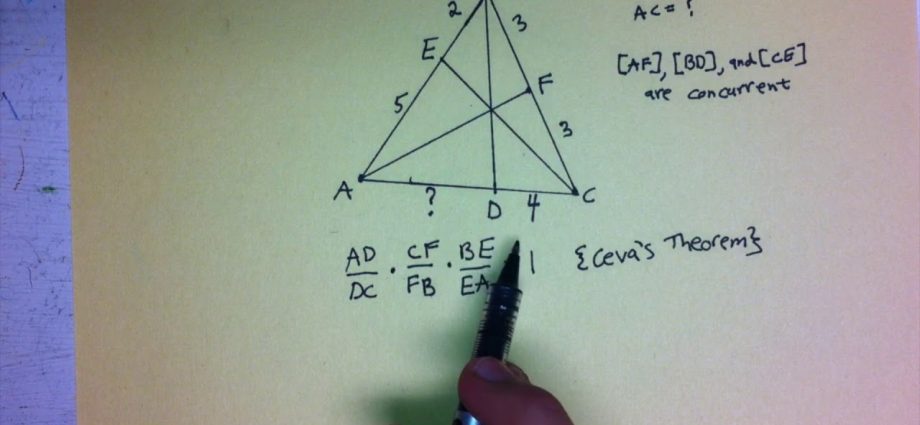
Example of a problem
Triangle given ABC with dots TO’, B ‘ и C ‘ on the sides BC, AC и AB, respectively. The vertices of the triangle are connected to the given points, and the formed segments pass through one point. At the same time, the points TO’ и B ‘ taken at the midpoints of the corresponding opposite sides. Find out in what ratio the point C ‘ divides the side AB.
Solution
Let’s draw a drawing according to the conditions of the problem. For our convenience, we adopt the following notation:
- AB’ = B’C = a
- BA’ = A’C = b
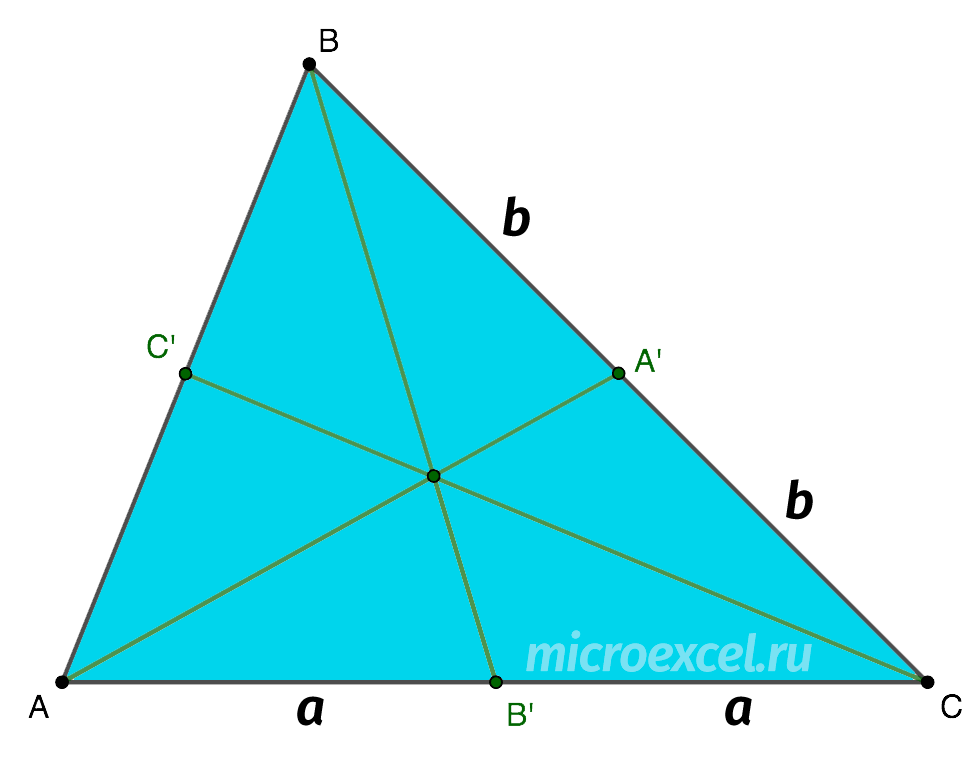
It remains only to compose the ratio of the segments according to the Ceva theorem and substitute the accepted notation into it:
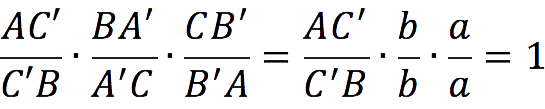
After reducing the fractions, we get:
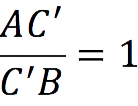
Hence, AC’ = C’B, i.e. point C ‘ divides the side AB in half.
Therefore, in our triangle, the segments AA’, BB’ и CC’ are medians. Having solved the problem, we proved that they intersect at one point (valid for any triangle).
Note: using Ceva’s theorem, one can prove that in a triangle at one point, the bisectors or heights also intersect.