In this publication, we will consider one of the main theorems in class 7 geometry – about the external angle of a triangle. We will also analyze examples of solving problems in order to consolidate the presented material.
Definition of an outside corner
First, let’s remember what an external corner is. Let’s say we have a triangle:
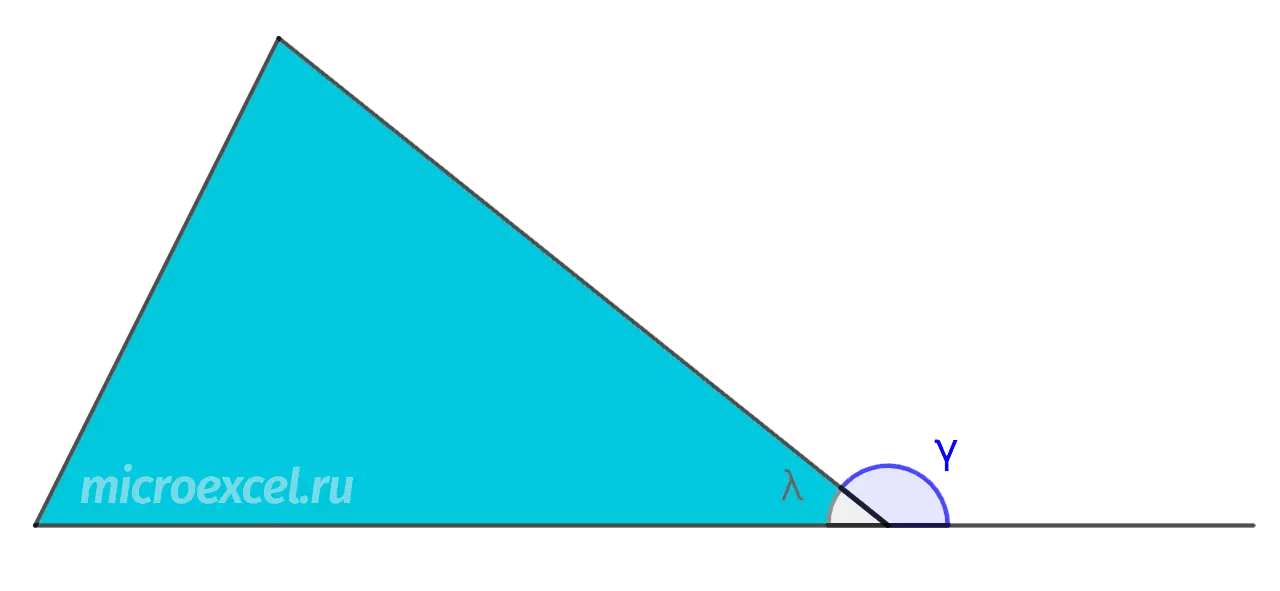
Adjacent to an internal corner (λ) triangle angle at the same vertex is external. In our figure, it is indicated by the letter γ.
Wherein:
- the sum of these angles is 180 degrees, i.e. c + λ = 180° (property of the outer corner);
- 0 и 0.
Statement of the theorem
The exterior angle of a triangle is equal to the sum of the two angles of the triangle that are not adjacent to it.
c = a + b

From this theorem it follows that the external angle of a triangle is greater than any of the internal angles that are not adjacent to it.
Examples of tasks
Task 1
A triangle is given in which the values of two angles are known – 45 ° and 58 °. Find the exterior angle adjacent to the unknown angle of the triangle.
Solution
Using the formula of the theorem, we get: 45° + 58° = 103°.
Task 1
The external angle of a triangle is 115°, and one of the non-adjacent internal angles is 28°. Calculate the values of the remaining angles of the triangle.
Solution
For convenience, we will use the notation shown in the figures above. The known internal angle is taken as α.
Based on the theorem: β = γ – α = 115° – 28° = 87°.
Angle λ is adjacent to the outer, and therefore is calculated by the following formula (follows from the property of the outer corner): λ = 180° – γ = 180° – 115° = 65°.









