Contents
In this publication, we will consider the definition, geometric interpretation, graph of a function, and examples of the modulus of a positive/negative number and zero.
Determining the modulus of a number
Real Number Modulus (sometimes called absolute value) is a value equal to it if the number is positive or equal to the opposite if it is negative.
The absolute value of a number a indicated by vertical lines on both sides of it – |a|.

opposite number differs from the original sign. For example, for the number 5 the opposite is -5. In this case, zero is opposite to itself, i.e.
Geometric interpretation of the module
Modulus of a is the distance from the origin (O) to a point A on the coordinate axis, which corresponds to the number aIe
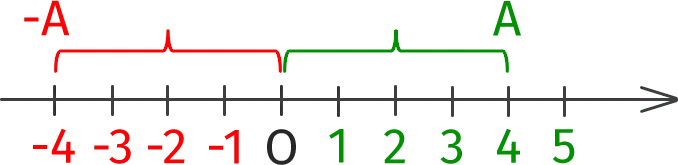
|-4| = |4| = 4
Function Graph with Modulus
Graph of an even function y = |х| as follows:
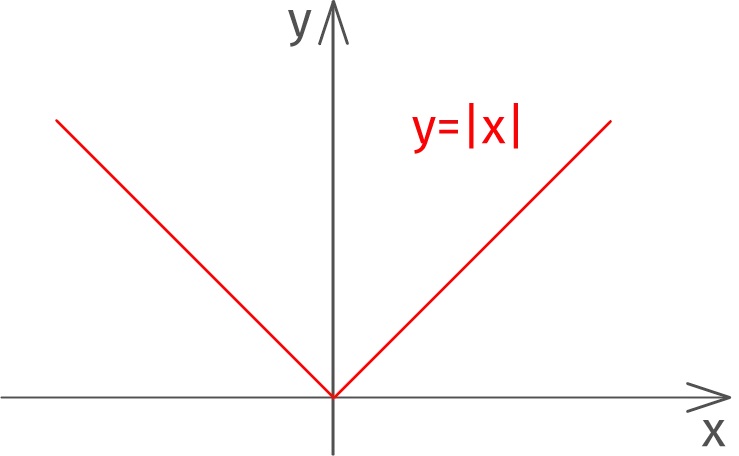
- y=x with x> 0
- y = -x with x
- y = 0 with x = 0
- domain of definition: (−∞;+∞)
- range: [0;+∞).
- at x = 0 the chart breaks.
Example of a problem
What are the following modules |3|, |-7|, |12,4| and |-0,87|.
Decision:
According to the above definition:
- |3| = 3
- |-7| = 7
- |12,4| = 12,4
- |-0,87| = 0,87









