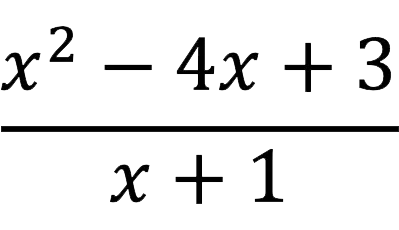What is the limit of a function

In this publication, we will consider one of the main concepts of mathematical analysis – the limit of a function: its definition, as well as various solutions with practical examples.

Determining the limit of a function

Function limit – the value to which the value of this function tends when its argument tends to the limiting point.

Limit record:

• the limit is indicated by the icon lim;
• below it is added what value the argument (variable) of the function tends to. Usually this x, but not necessarily, for example:x→1″;
• then the function itself is added on the right, for example:

  

Thus, the final record of the limit looks like this (in our case):

Reads like “limit of the function as x tends to unity”.

x→ 1 – this means that “x” consistently takes on values ​​that infinitely approach unity, but will never coincide with it (it will not be reached).

Decision limits

With a given number

Let’s solve the above limit. To do this, simply substitute the unit in the function (because x→1):

Thus, to solve the limit, we first try to simply substitute the given number into the function below it (if x tends to a specific number).

With infinity

In this case, the argument of the function increases infinitely, that is, “x” tends to infinity (∞). For example:

If x→∞, then the given function tends to minus infinity (-∞), because:

• 3 – 1 = 2
• 3 – 10 = -7
• 3 – 100 = -97
• 3 – 1000 – 997 etc.

Another more complex example

In order to solve this limit, also, simply increase the values x and look at the “behavior” of the function in this case.

• RџSЂRё x = 1, y = 1² + 3 · 1 – 6 = -2
• RџSЂRё x = 10, y = 10² + 3 · 10 – 6 = 124
• RџSЂRё x = 100, y = 100² + 3 · 100 – 6 = 10294

Thus, for “x”tending to infinity, the function x² + 3x – 6 grows indefinitely.

With uncertainty (x tends to infinity)

In this case, we are talking about limits, when the function is a fraction, the numerator and denominator of which are polynomials. Wherein “x” tends to infinity.

Example: let’s calculate the limit below.

Solution

The expressions in both the numerator and the denominator tend to infinity. It can be assumed that in this case the solution will be as follows:

However, not all so simple. To solve the limit we need to do the following:

1. Find x to the highest power for the numerator (in our case, it’s two).

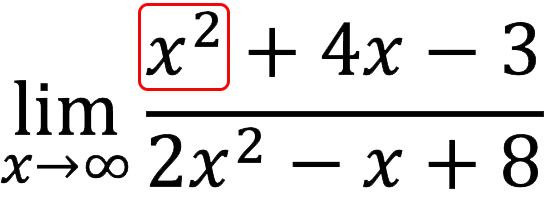
2. Similarly, we define x to the highest power for the denominator (also equals two).

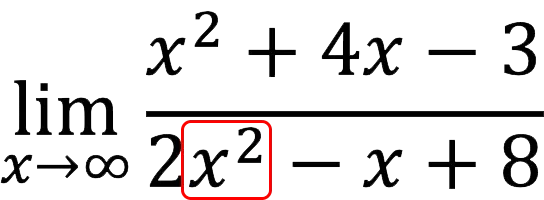
3. Now we divide both the numerator and the denominator by x in senior degree. In our case, in both cases – in the second, but if they were different, we should take the highest degree.

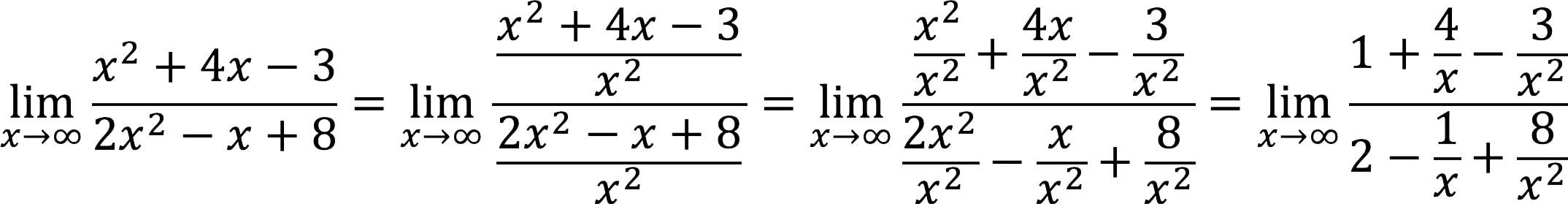
4. In the resulting result, all fractions tend to zero, therefore the answer is 1/2.

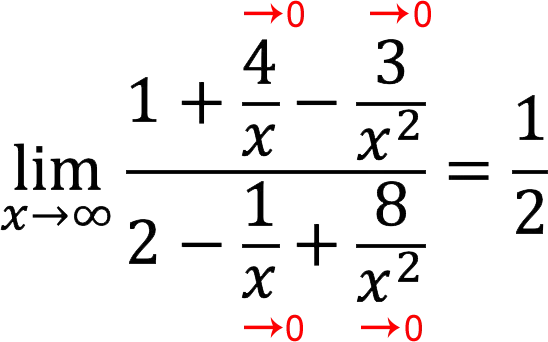
With uncertainty (x tends to a specific number)

Both the numerator and the denominator are polynomials, however, “x” tends to a specific number, not to infinity.

In this case, we conditionally close our eyes to the fact that the denominator is zero.

Example: Let’s find the limit of the function below.

Solution

1. First, let’s substitute the number 1 into the function, to which “x”. We get the uncertainty of the form we are considering.

2. Next, we decompose the numerator and denominator into factors. To do this, you can use the abbreviated multiplication formulas, if they are suitable, or.

In our case, the roots of the expression in the numerator (2x² – 5x + 3 = 0) are the numbers 1 and 1,5. Therefore, it can be represented as: 2(x-1)(x-1,5).

Denominator (x–1) is initially simple.

3. We get such a modified limit:

4. The fraction can be reduced by (x–1):

5. It remains only to substitute the number 1 in the expression obtained under the limit: