In this publication, we will consider what a segment is, list its main properties, and also give possible options for the location of two segments in relation to each other on a plane.
Line definition
Line segment is the part bounded by two points on it.
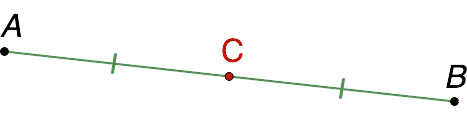
A segment has a beginning and an end, and the distance between them is called its long.
Usually, a segment is denoted by two large Latin letters, which correspond to points on the line (or its ends), and it does not matter in what order. For example, AB or BA (these segments are the same).
If the order is important, then such a segment is called directed. In this case, segments AB and BA do not coincide.
midpoint is a point (in our case, C) that bisects it

Mutual arrangement of segments
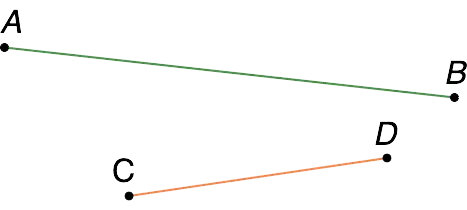
Two segments on a plane, like straight lines, can be:
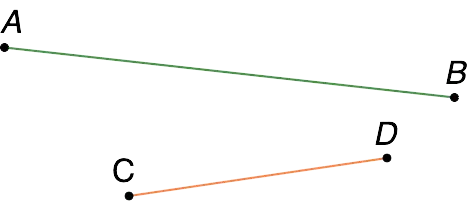
- parallel (do not intersect);

- intersecting (there is one common point);

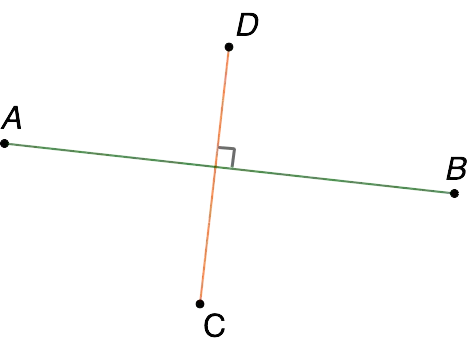
- perpendicular (located at right angles to each other).

Note: unlike straight lines, two line segments may not be parallel, and at the same time they may not intersect.
Line Properties
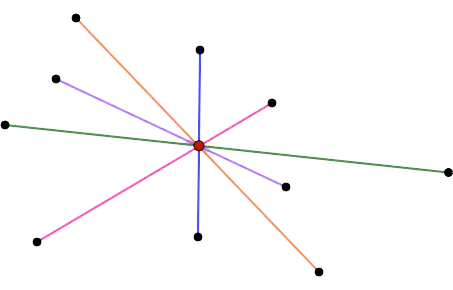
- An infinite number of line segments can be drawn through any point.

- Any two points form a line segment.
- The same point can be the end of an infinite number of segments.

- Two segments are considered equal if their lengths are equal. That is, when one is superimposed on the other, both their ends will coincide.
- If some point divides a segment into two, then the length of this segment is equal to the sum of the lengths of the other two
(AB = AC + CB) .
- If any two points of a segment belong to the same plane, then all points of this segment lie on the same plane.