In this publication, we will consider the definition, elements, types and main properties of a parallelepiped, incl. rectangular. The presented information is accompanied by visual drawings for better perception.
Definition of a box
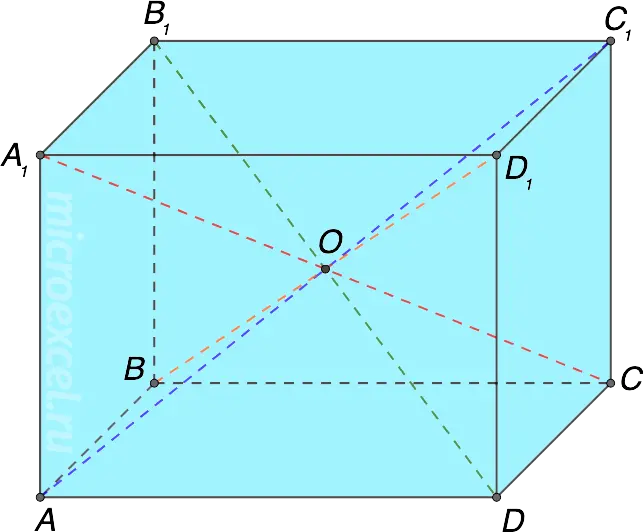
Parallelepiped is a geometric figure in space; a hexagon whose faces are parallelograms. The figure has 12 edges and 6 faces.
A parallelepiped is a variety with a parallelogram as bases. The main elements of the figure are the same as those of the prism.
Note: Formulas for calculating (for a rectangular figure) and a parallelepiped are presented in separate publications.
Types of parallelepipeds
- Straight parallelepiped – the side faces of the figure are perpendicular to its bases and are rectangles.

- A right parallelepiped can be rectangular The bases are rectangles.

- Oblique parallelepiped – side faces are not perpendicular to the bases.

- – all sides of the figure are equal squares.

- If all faces of a parallelepiped are identical rhombuses, it is called rhombohedron.
Box properties
1. Opposite faces of a parallelepiped are mutually parallel and are equal parallelograms.
2. All diagonals of the parallelepiped intersect at one point and are divided in half at it.
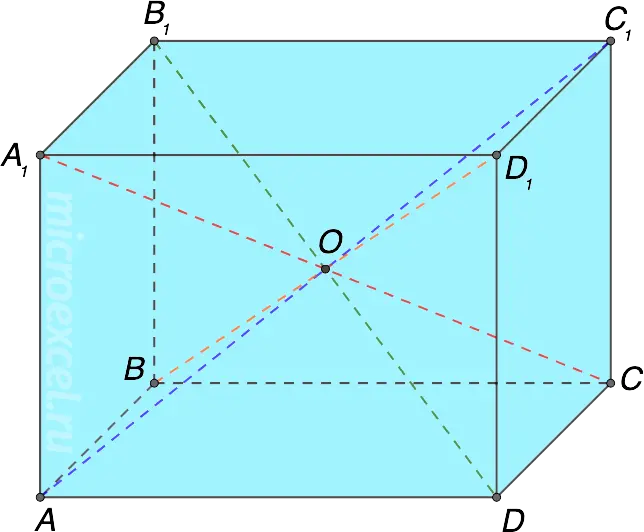
3. Square diagonal (D) of a rectangular parallelepiped is equal to the sum of the squares of its three dimensions: the length (a), width (B) and heights (C).
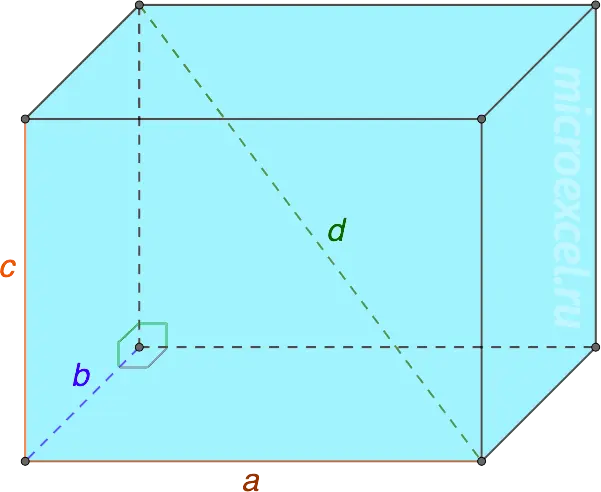
d2 = A2 + b2 + c2
Note: to the parallelepiped, also apply.