In this publication, we will consider the definition and main elements of a matrix with examples, its scope, and also provide a brief historical background regarding the development of matrix theory.
Matrix Definition
Matrix is a kind of rectangular table that consists of rows and columns containing certain elements.
Matrix size sets the number of rows and columns, which are indicated by letters m и n, respectively. The table itself is framed by round brackets (sometimes square brackets) or one/two parallel vertical lines.
The matrix is denoted by a capital letter A, and together with an indication of its size – Amn. An example is shown below:
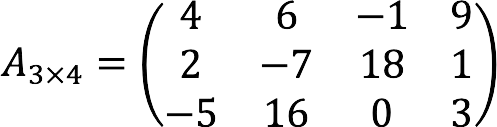
Application of matrices in mathematics
Matrices are used to write and solve or systems of differential equations.
Matrix elements
To denote the elements of the matrix, the standard notation is used aij, where:
- i – number of the line containing the given element;
- j – respectively, column number.
For example, for the matrix above:
- a24 = 1 (second row, fourth column);
- a32 = 16 (third row, second column).
Rows
If all elements of a matrix row are equal to zero, then such a row is called null (highlighted in green).
![]()
Otherwise, the line is nonzero (highlighted in red).
Diagonals
The diagonal drawn from the upper left corner of the matrix to the lower right is called the main.

If a diagonal is drawn from the bottom left to the top right, it is called collateral.

Historical information
“Magic Square” – under this name, matrices were first mentioned in ancient China, and later among Arab mathematicians.
In 1751 the Swiss mathematician Gabriel Cramer published “Kramer’s rule”used to solve systems of linear algebraic equations (SLAE). Approximately at the same time, the “Gauss method” appeared for solving SLAE by sequential elimination of variables (the author is Carl Friedrich Gauss).
A significant contribution to the development of matrix theory was also made by such mathematicians as William Hamilton, Arthur Cayley, Karl Weierstrass, Ferdinand Frobenius and Marie Enmond Camille Jordan. The very same term “matrix” in 1850 was introduced by James Sylvester.









