In this publication, we will consider what complex conjugate numbers are, and also list their main properties. The theoretical information presented is accompanied by practical examples for better understanding.
Definition of complex conjugate numbers
Given a complex number
Thus, for complex conjugate numbers, the real parts are the same, and the imaginary parts differ in sign.
Example:
For a number
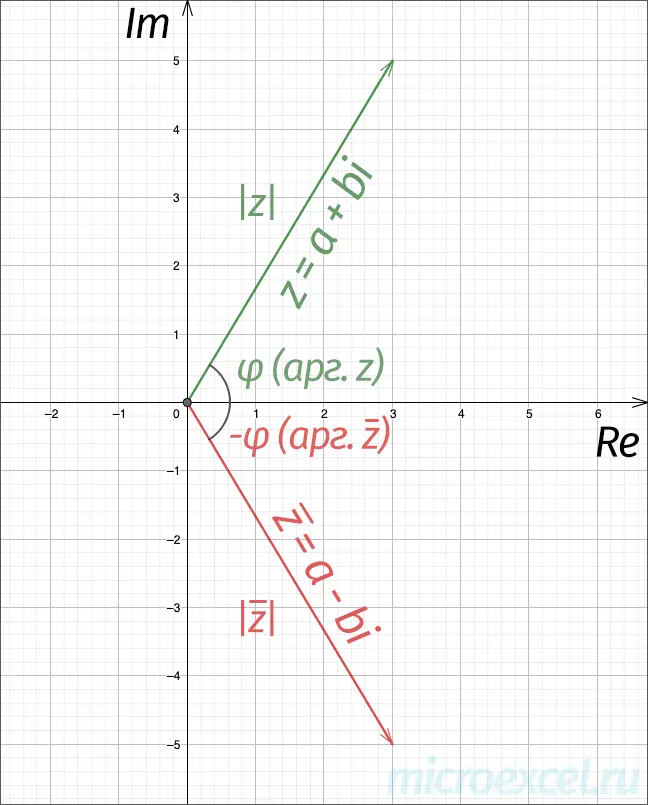
Geometric interpretation
If we transfer complex conjugate numbers to the complex plane, then they will be a mirror image of each other about the real axis (RE).
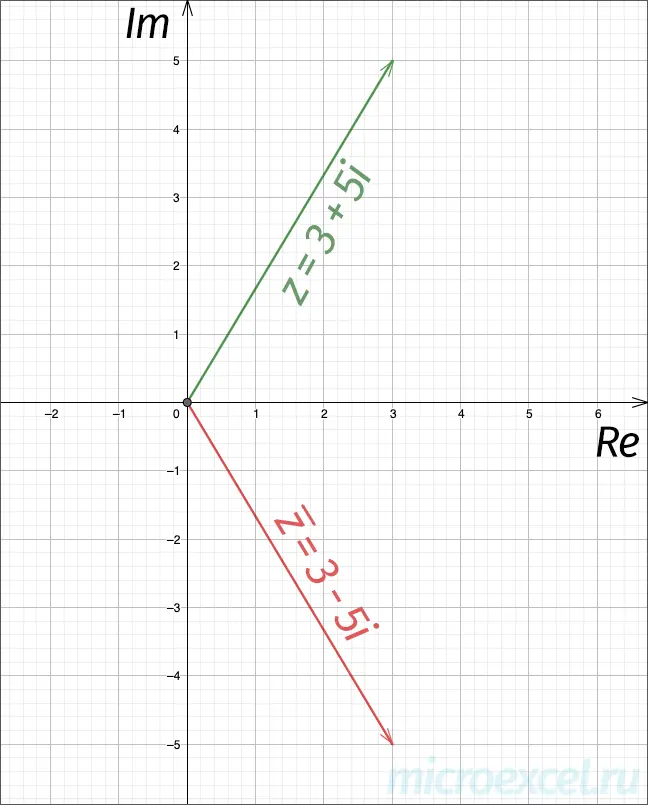
Properties of complex conjugate numbers
1. If z = z, means the number z is valid.
Example:
z = 2, so
2. complex conjugate numbers are equal, i.e.
3. The sum of complex conjugate numbers is a real number:
Example:
z=5+2i
z = 5 – 2i
4. The product of complex conjugate numbers is equal to the square of their modulus and is a real number:
Example:
z = 6 – 4i
z = 6 + 4i
with ⋅ z =
The module is considered as follows:
![]()
5 For
![]()
6. For arbitrary complex numbers z1 и z2:
» data-order=» » style=»min-width:64.4914%; width:64.4914%;»>
» style=»min-width:64.4914%; width:64.4914%;»>
» data-order=» «>
«>
» data-order=»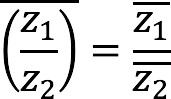 «>
«>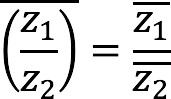
| Addition and subtraction |
| Multiplication |
| Division |









