Contents
In this publication, we will consider what the adjacent angles are, give the formulation of the theorem regarding them (including the consequences from it), and also list the trigonometric properties of adjacent angles.
Definition of adjacent corners
Two adjacent angles that form a straight line with their outer sides are called adjacent. In the figure below, these are the corners α и β.
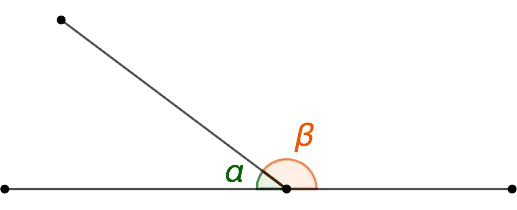
If two corners share the same vertex and side, they are adjacent. In this case, the inner regions of these corners should not intersect.
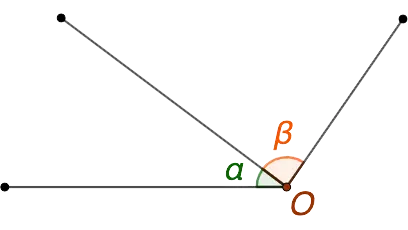
The principle of constructing an adjacent corner
We extend one of the sides of the corner through the vertex further, as a result of which a new corner is formed, adjacent to the original one.
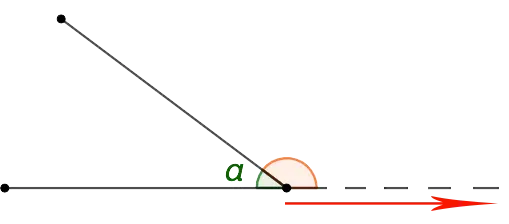
Adjacent angle theorem
The sum of the degrees of adjacent angles is 180°.
Adjacent corner 1 + Adjacent angle 2 = 180°
Example 1
One of the adjacent angles is 92°, what is the other one?
The solution, according to the theorem discussed above, is obvious:
Adjacent angle 2 = 180° – Adjacent angle 1 = 180° – 92° = 88°.
Consequences from the theorem:
- Adjacent angles of two equal angles are equal to each other.
- If an angle is adjacent to a right angle (90°), then it is also 90°.
- If the angle is adjacent to an acute one, then it is greater than 90°, i.e. is dumb (and vice versa).
Example 2
Let’s say we have an angle adjacent to 75°. It must be greater than 90°. Let’s check it out.
Using the theorem, we find the value of the second angle:
180° – 75° = 105°.
105° > 90°, hence the angle is obtuse.
Trigonometric properties of adjacent angles
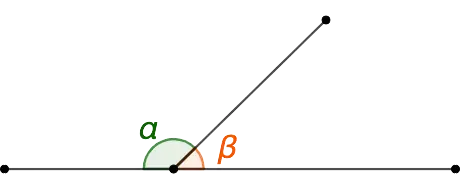
- The sines of adjacent angles are equal, i.e. sin α = sin β.
- The values of the cosines and tangents of adjacent angles are equal, but have opposite signs (except for undefined values).
- cos α = -cos β.
- tg α = -tg β.









