Not very common, but not exotic either. At my trainings, this question was asked more than once or twice 🙂 The bottom line is that we have a finite set of some numbers, from which we need to choose those that will add up to a given value.
In real life, this task may look different.
- For example, we have downloaded from the Internet bank all the payments that have been received on our account for the last month. One of the clients splits the amount of his payment into several separate accounts and pays in installments. We know the total payment amount and the number of invoices, but we do not know their amounts. It is necessary to select those amounts in the payment history that will give a generally given value.
- We have several rolls of steel (linoleum, paper…), from which we need to select those that will give a given length.
- Blackjack or popularly “point”. It is necessary to collect cards with a total value as close as possible to 21 points, but not exceed this threshold.
In some cases, the permissible tolerance error may be known. It can be either zero (in the case of picking accounts), or non-zero (in the case of picking rolls), or bounded from the bottom or from the top (in the case of blackjack).
Let’s take a look at several ways to solve such a task in Excel.
Method 1. Add-in Search for a solution (Solver)
This add-in is included in the standard set of Microsoft Office along with Excel and is intended, in general, to solve linear and nonlinear optimization problems with a list of constraints. To connect it, you must:
- in Excel 2007 and newer go File – Excel Options – Add-ins – Go
- in Excel 2003 and older – open the menu Tools – Add-ins
and check the corresponding box. Then on a tab or in a menu Data the command we need will appear.
To use the add-on Search Solutions for our task, it will be necessary to slightly modernize our example by adding several auxiliary cells and formulas to the list of sums to be selected:
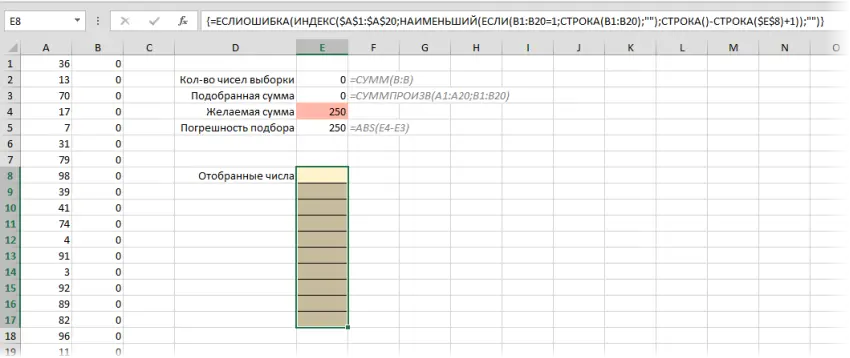
- Range A1: A20 contains our numbers, from which we will choose the ones we need to “fit” into the given amount.
- Range B1: B20 will be a kind of set of switches, i.e. will contain zeros or ones, indicating whether we are selecting a given number in the sample or not.
- In a cell E2 there is the usual auto-sum of all units in column B, which counts the number of selected numbers.
- In a cell E3 using the function SUMPRODUCT the sum of pairwise products of cells from columns A and B is calculated (ie A1*B1+A2*B2+A3*B3+…). In fact, here the sum of the numbers from column A, selected by ones from column B, is calculated.
- Into a pink cell E4 the user enters the desired amount for picking.
- In a cell E5 the absolute value of the selection error is calculated in order to minimize it in the future.
- All yellow cells E8: E17 I would like to get a list of selected numbers, i.e. those numbers from column A, opposite which there are ones in column B. To do this, select all (!) yellow cells at once and enter the following array formula in them:
=ЕСЛИОШИБКА(ИНДЕКС($A$1:$A$20;НАИМЕНЬШИЙ(ЕСЛИ(B1:B20=1;СТРОКА(B1:B20);»»);СТРОКА()-СТРОКА($E$8)+1));»»)
=IFERROR(INDEX($A$1:$A$20;SMALL(IF(B1:B20=1;ROW(B1:B20);»»);ROW()-ROW($E$8)+1));»»)
After entering the formula, it must be entered not as an ordinary formula, but as an array formula, i.e. press not Enter, but Ctrl + Shift + Enter. A similar formula is used in the VLOOKUP example, which returns all found values at once (not just the first).
Now let’s go to the tab (or menu) Data and run the tool Search for a solution (Data – Solver):
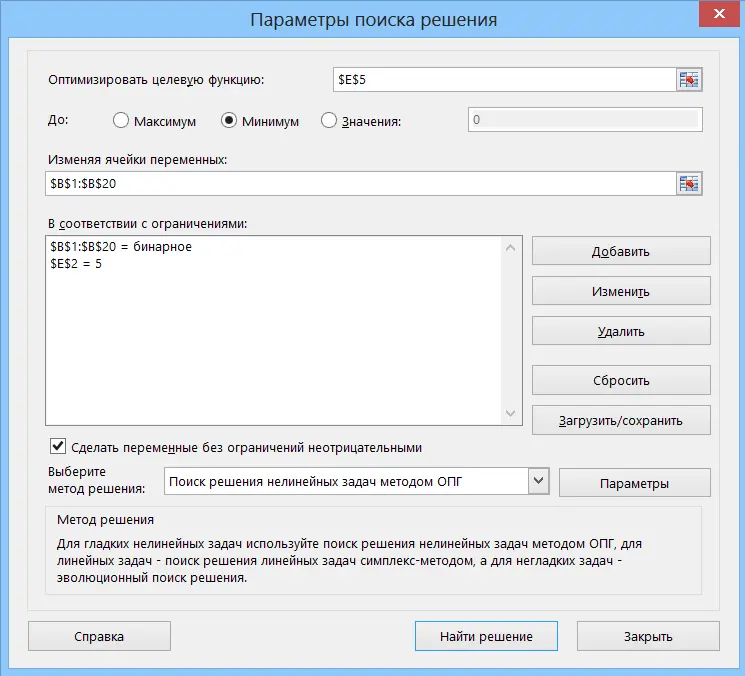
In the window that opens, you need to:
- Set as the target function (Target Cell) – the cell for calculating the selection error E5. Just below select the option – Minimumsince we want to select numbers for a given amount with a minimum (or even better zero) error.
- Set the range of the radio button column B1: B20 as the Changing cells.
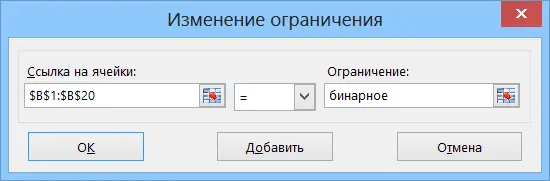
- Using the button Add create an additional condition that the cells of the range B1: B20 must be binary (i.e. contain only 0 or 1):
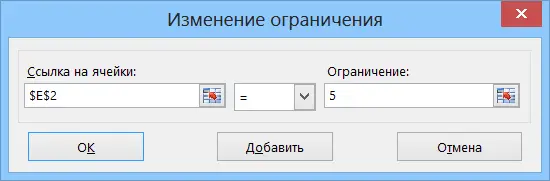
- Using the same button, if necessary, create a limit on the number of numbers in the sample. For example, if we know that the amount has been split into 5 accounts, then:
After entering all the parameters and restrictions, we start the selection process with the button Find a solution (Solve)… The selection process takes from several seconds to several minutes (in severe cases) and ends with the appearance of the following window:
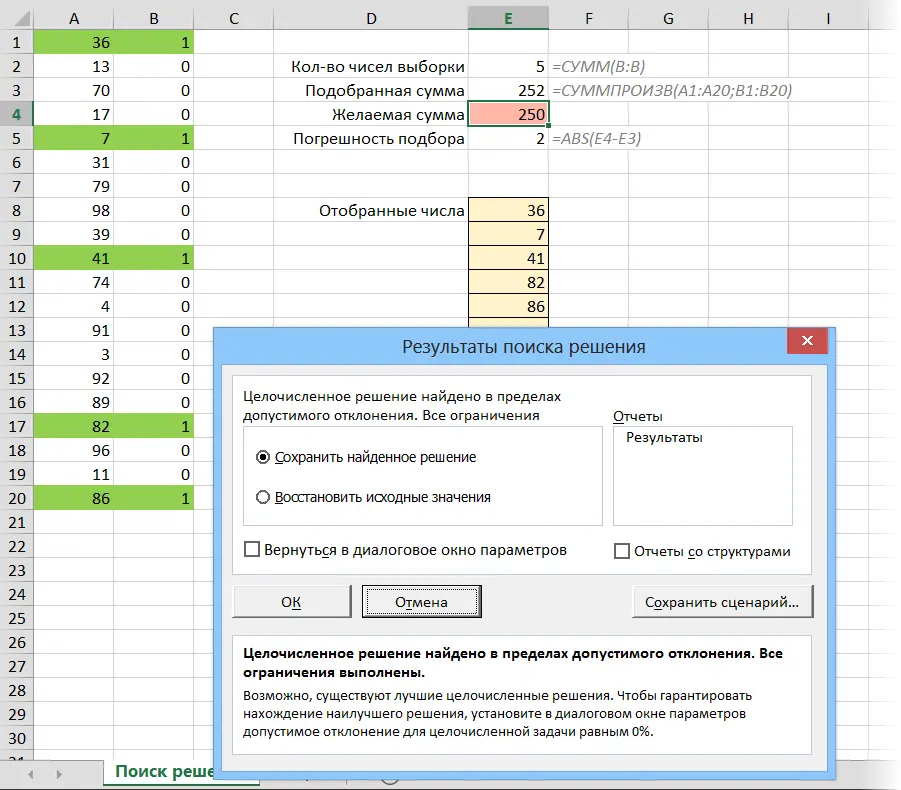
Now you can either leave the found selection solution (Save found solution), or roll back to the previous values (Restore original values).
It should be noted that for this class of problems there is not one, but a whole set of solutions, especially if the error is not strictly equated to zero. Therefore launching Finding a solution with different initial data (i.e. different combinations of 0 and 1 in column B) can lead to different sets of numbers in the samples within the given constraints. So it makes sense to run this routine a few times, arbitrarily changing the switches in column B.
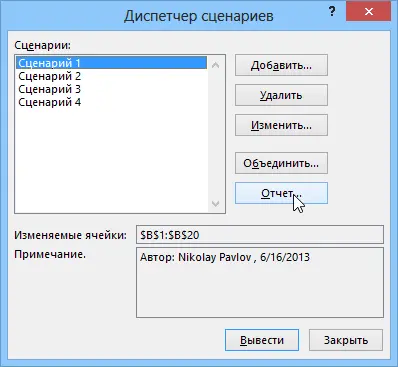
Found combinations can be saved as scripts (button Save script) to return to it later with the command Data – What-If Analysis – Scenario Manager (Data – What-If Analysis – Scenario Manager):
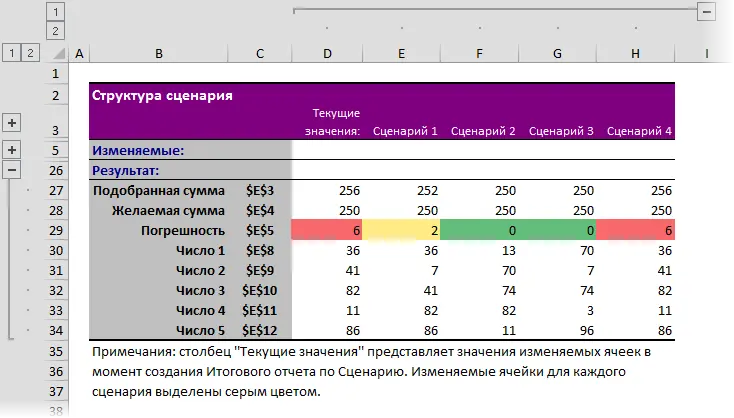
And it will be very convenient to display all the solutions found, saved as scripts, in one comparison table using the button Report (Summary):
Method 2. Macro selection
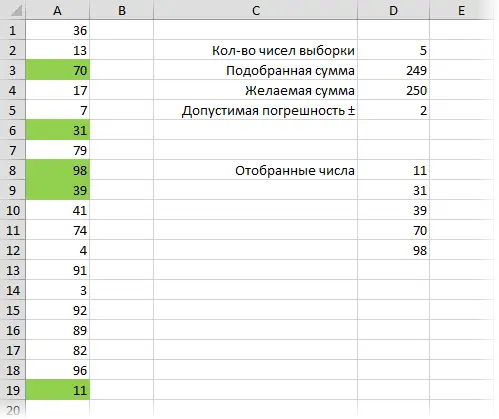
In this method, all the work is done by a macro that stupidly iterates over random combinations of numbers until it stumbles upon the required amount within the allowed error. You don’t need to add a column with zeros and ones and formulas in this case.
To use the macro, press Alt + F11, in the Visual Basic editor window that opens, insert a new module through the menu Insert – Module and copy this code there:
Sub Combinator() Dim Data() As Variant, Selected() As Variant Dim goal As Double, sel_count As Integer, prec As Double Const LIMIT = 1000000 prec = Range("D5").Value sel_count = Range("D2") .Value goal = Range("D4").Value Set OutRange = Range("D8") Set InputRange = Range("A1", Range("A1").End(xlDown)) input_count = InputRange.Cells.Count Data = InputRange.Value ReDim Selected(1 To sel_count) As Variant NewTry: For j = 1 To sel_count Start: RandomIndex = Int(Rnd * input_count + 1) RandomValue = Data(RandomIndex, 1) this has not been selected already If j > 1 Then For k = 1 To j - 1 If Selected(k) = RandomValue Then GoTo Start Next k End If Selected(j) = RandomValue Next j If Abs(WorksheetFunction.Sum(Selected) - goal) <= prec Then Range("D3").Value = WorksheetFunction.Sum(Selected) MsgBox "Getting completed. Desired accuracy achieved." Range(OutRange, OutRange.End(xlDown)).ClearContents OutRange.Resize(sel_count, 1).Value = Application.Transpose(Selected) Exit Sub Else iterations = iterations + 1 If iterations > LIMIT Then MsgBox "Try limit reached. Solution not found." Exit Sub Else Go To New Try End If End If End Sub Similarly to the first method, by running the macro several times, you can get different sets of suitable numbers.
PS Now enthusiasts from the Mekhmat of Moscow State University will run up with shouts of “Stupid bust – this is unaesthetic!” Yes, I am aware that brute force search is not the best way to search. Yes, there are many smart algorithms for finding solutions to such problems that reduce the search time and find the right combination much faster. I can even talk about a couple. But at this stage, the existing speed of “dumb enumeration” is quite enough for me – processing an array of 1000 cells takes less than a second. Ready to wait 🙂
- Optimize your business model with the Solver add-in
- What are macros, where and how to insert macro code in VBA