In this publication, we consider the basic minor theorem (statement and corollaries). We will also analyze an example of a problem to demonstrate its application in practice.
Statement of the theorem
In an arbitrary matrix A columns/rows that are part of the basis minor M (called “basic”) are linearly independent. Each column/row of the matrix is a linear combination of the underlying columns/rows.
Granted, given the matrix A size mxn. basic is called a non-zero minor M order r, while all minors of higher order (r+1 and above) are equal to zero or none at all. It means that r equals the smallest number m or n.
From the basic minor theorem it follows:
- Linearly independent columns/rows of a matrix, the number of which is equal to the given matrix, are basic.
- The rank of any matrix is equal to the maximum number of linearly independent rows/columns contained in it.
Example of a problem
Let’s find all the basis minors of the matrix A, presented below, and also determine its rank.
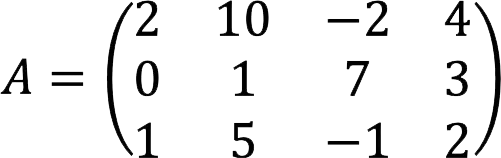
Decision:
1. Let’s execute on the matrix to simplify it. To begin with, we divide the third row by 2 and rearrange it with the first places.
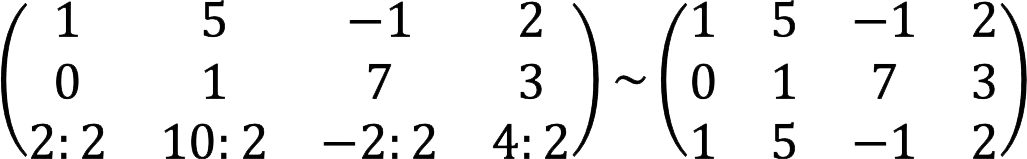
2. Subtract the first line from the third line.
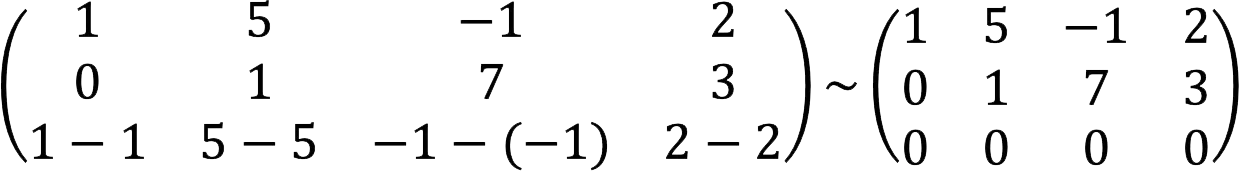
3. We get a matrix with a zero row, which means that all third-order minors are equal to zero.
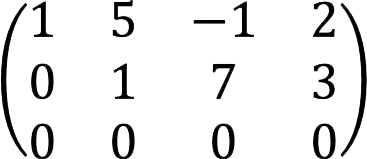
4. Thus, in our case, only non-zero second-order minors, consisting of the first and second rows of the resulting matrix, can be basic.
![]()
![]()
![]()
![]()
![]()
![]()
Answer:
All calculated minors are different from zero, which means that they are all basic. Matrix rank is two









