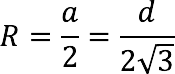In this publication, we will consider how you can find the radius of a ball (sphere) inscribed in a cube if the length of the cube edge or its diagonal is known.
Note: Recall that in any one can enter .
Let’s start with a drawing.
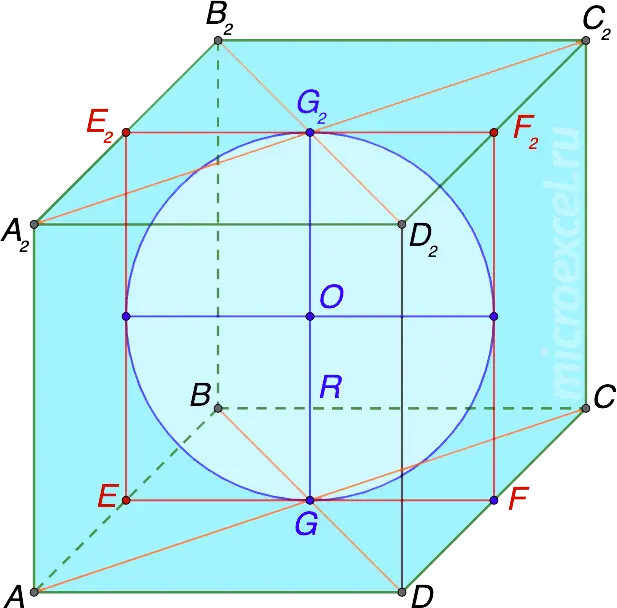
- the ball touches all 6 faces of the cube (only 4 touch points are shown in the figure);
- the center of the ball is a point O, which is also the center of the cube.
Ball radius (R) inscribed in a cube is equal to half of its edge, i.e.:
R = a/2Where “to” – the edge of the cube (is the side of its face).
To make it clearer, let’s do section, parallel to one of the faces of the cube and passing through the points of contact of the ball of two other faces parallel to each other. This section also passes through the midpoints of the respective sides.
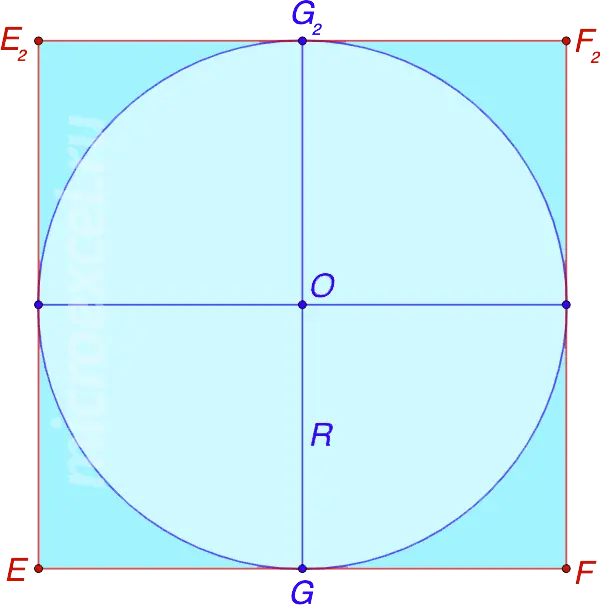
Thus, we get a square with an inscribed circle, the radius of which is equal to half of its side, which in turn is equal to the edge of the cube.
Radius of an inscribed sphere through the diagonal of a cube
If the length of the diagonal of the cube is known (we will take it as “d”), the radius of the ball inscribed in it (R) can be calculated as follows: