In this publication, we will consider how to find the radius of a ball (sphere) inscribed in a cone, as well as its surface area and volume.
Finding the Radius of a Ball/Sphere
Any cone can be inscribed. In other words, around any ball can be described.
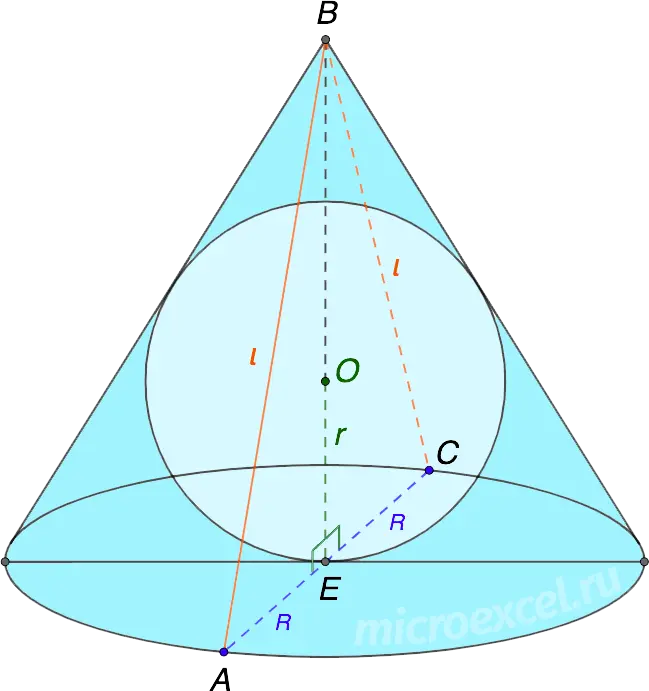
To find the radius of a ball (sphere) inscribed in a cone, we draw an axial section of the cone. Thus, we get an isosceles triangle (in our case – ABC), in which a circle with a radius is inscribed r.
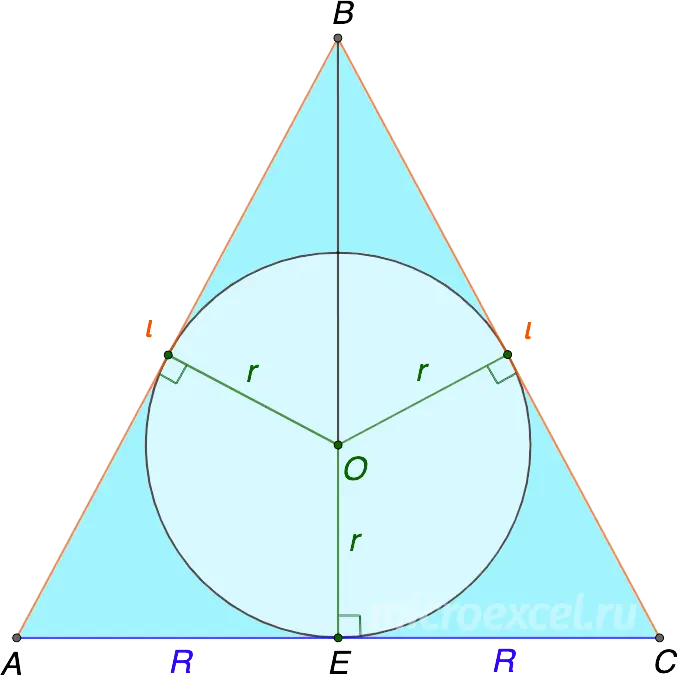
Cone base radius (R) equals half the base of the given triangle (B.C), and generators (l) are its lateral sides (AB и BC).
Radius of a circle inscribed in an isosceles triangle ABC, among other things, is the radius of a sphere inscribed in a cone. It is found according to the formula:
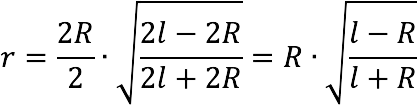
Formulas for area and volume of a ball/sphere
Knowing the radius (r) you can find the surface area (S) spheres and volume (V) sphere bounded by this sphere:
![]()
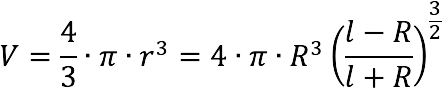
Note: π rounded equals 3,14.









