Finding the inverse matrix

In this publication, we will consider what an inverse matrix is, and also, using a practical example, we will analyze how it can be found using a special formula and an algorithm for sequential actions.

Definition of inverse matrix

First, let’s remember what reciprocals are in mathematics. Let’s say we have the number 7. Then its inverse will be 7^-1 or ¹/₇. If you multiply these numbers, the result will be one, i.e. 7 7^-1 = 1.

Almost the same with matrices. Reverse such a matrix is ​​called, multiplying which by the original one, we get the identity one. She is labeled as A^-1.

A · A^-1 =E

Algorithm for finding the inverse matrix

To find the inverse matrix, you need to be able to calculate matrices, as well as have the skills to perform certain actions with them.

It should be noted right away that the inverse can only be found for a square matrix, and this is done using the formula below:

|A| – matrix determinant;

A^T_M is the transposed matrix of algebraic additions.

Note: if the determinant is zero, then the inverse matrix does not exist.

Example

Let’s find for the matrix A below is the reverse of it.

Solution

1. First, let’s find the determinant of the given matrix.

2. Now let’s make a matrix that has the same dimensions as the original one:

We need to figure out which numbers should replace the asterisks. Let’s start with the top left element of the matrix. The minor to it is found by crossing out the row and column in which it is located, i.e. in both cases at number one.

The number that remains after the strikethrough is the required minor, i.e. M₁₁ = 8.

Similarly, we find the minors for the remaining elements of the matrix and get the following result.

3. We define the matrix of algebraic additions. How to calculate them for each element, we considered in a separate.

For example, for an element a₁₁ algebraic addition is considered as follows:

A₁₁ = (-1)^{1 + 1} M₁₁ = 1 · 8 = 8

4. Perform the transposition of the resulting matrix of algebraic additions (ie, swap the columns and rows).

5. It remains only to use the formula above to find the inverse matrix.

We can leave the answer in this form, without dividing the elements of the matrix by the number 11, since in this case we get ugly fractional numbers.

Checking the result

To make sure that we got the inverse of the original matrix, we can find their product, which should equal the identity matrix.

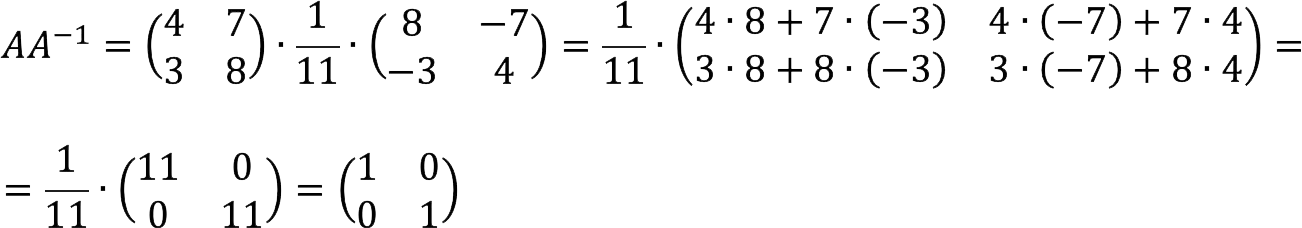
As a result, we got the identity matrix, which means we did everything right.