Contents
In this publication, we will consider various formulas with which you can calculate the height of a rectangular trapezoid.
Recall that one of the sides is perpendicular to its bases, and therefore it is also the height of the figure.
Finding the height of a rectangular trapezoid
Through the lengths of the sides
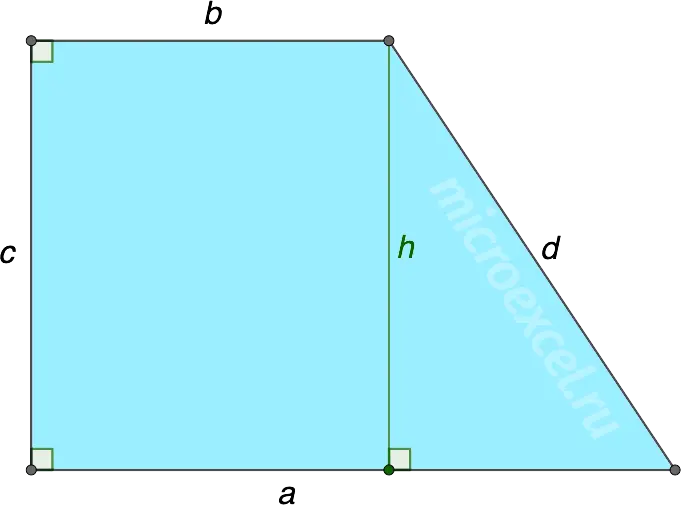
Knowing the lengths of both bases and the larger side of a rectangular trapezoid, you can find its height (or smaller side):
![]()
This formula follows from . In this case, the height h is the unknown leg of a right triangle whose hypotenuse is d, and the known leg – the differences of the bases, i.e. (ab).
Through bases and adjacent angle
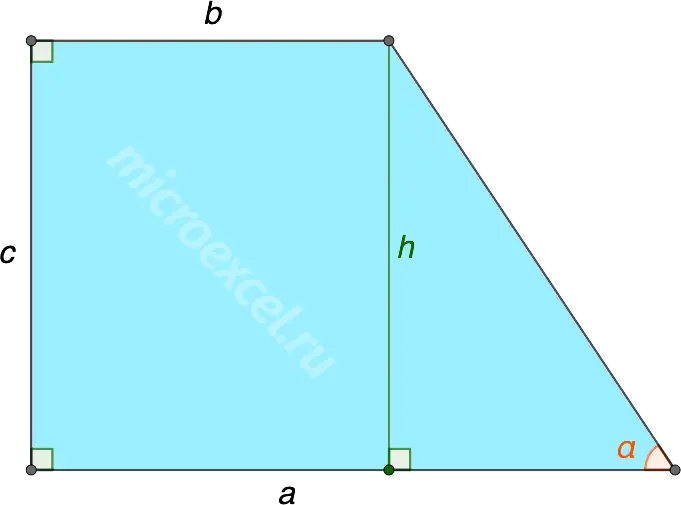
If the lengths of the bases and any of the acute angles adjacent to them are given, then the height of a rectangular trapezoid can be calculated using the formula:
![]()
Through the side and adjacent corner
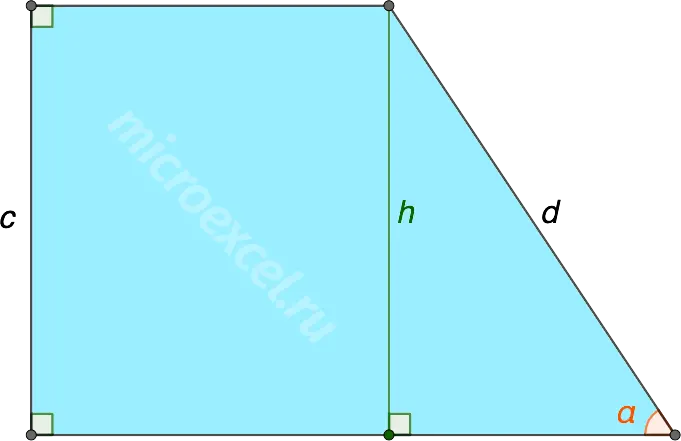
If the length of the lateral side of a rectangular trapezoid and the angle adjacent to it (any) are known, it will be possible to find the height of the figure in this way:
![]()
Note: using this formula, you can, among other things, prove that the smaller side is the height of the trapezoid:
![]()
Through the diagonals and the angle between them
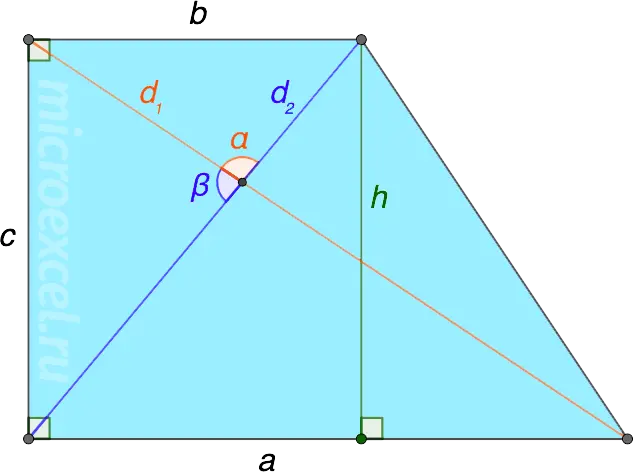
Provided that the lengths of the bases of a rectangular trapezoid, the diagonals and the angle between them are known, the height of the figure can be calculated as follows:
![]()
If instead of the sum of the bases, the length of the midline is known, then the formula will take the form:
![]()

m – the middle line, which is equal to half the sum of the bases, i.e.m = (a+b)/2.
Through area and grounds
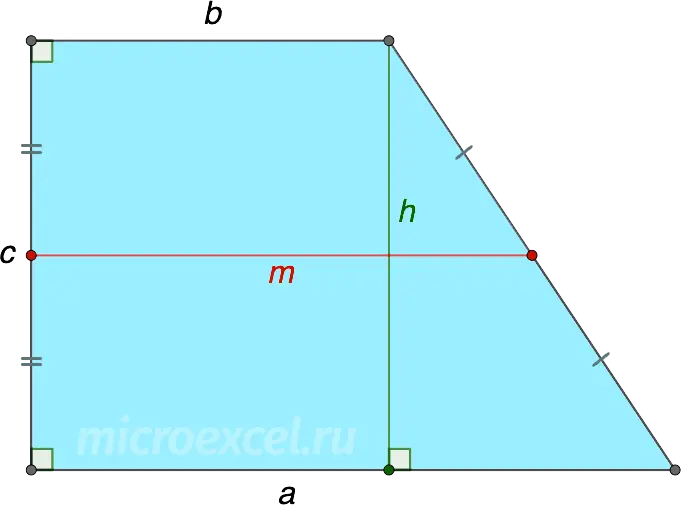
If you know the area of a rectangular trapezoid and the length of its bases (or midline), you can find the height in this way:
![]()









