Exponential function: definition, formula, properties, graph

In this publication, we will consider the definition and formula of the exponential function, list its main properties, and also demonstrate what its graph looks like and give an example of its construction.

Definition of exponential function

Exponential function is a function of the form f(x) = a ^x, where:

• a – the base of the degree, while a > 0 и a ≠ 1;
• x – exponent.

examples:

• y = 5 ^x
• y = 0,7 ^x
• y = 11 ^x

Properties of the exponential function

1. The domain of definition is all real numbers: – ∞ x +∞.
2. The range is all positive real numbers: 0 y +∞.
3. The function increases at a > 1 and decreases at 0 a <1.
4. For exponential functions are applicable.
5. Derivative:
   • (a ^x)‘= a ^x ln a
   • if instead of x more complex expression u: (a ^u)‘= a ^u ln a ⋅ u ‘
6. Integral:

   

Graph of an exponential function

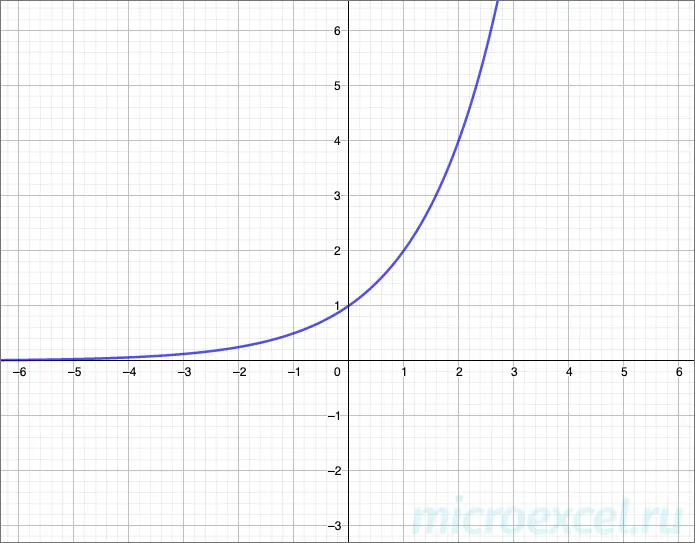
According to Property 3 above, the graph of an exponential function can be:

• increasing at a > 1:
• decreasing at 0 a < 1:

Asymptote – that’s it Ox, i.e. the graph line will tend to the x-axis, but will never touch it.

Example: build a graph of the function y = 3 ^x.

Decision:

First, let’s create a table of values ​​correspondence x и y.