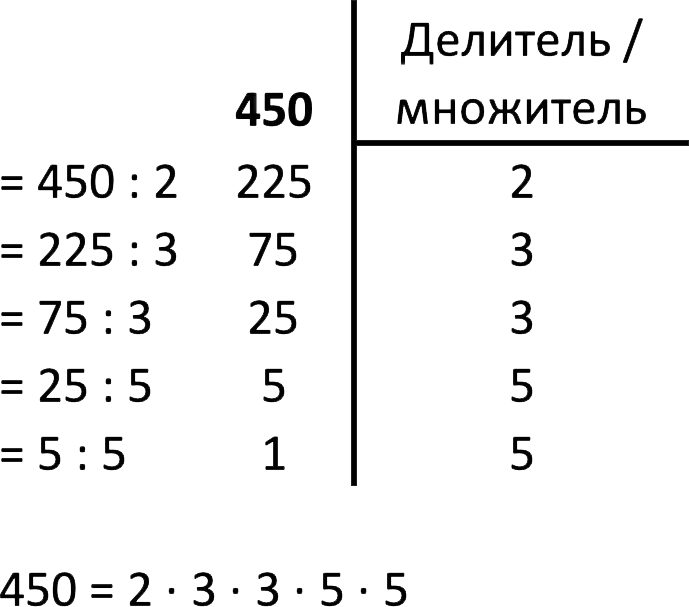In this publication, we will consider what prime factors are and how to decompose any number into them. We will accompany the theoretical material with examples for a better understanding.
Content
Algorithm for decomposing a number into prime factors
To begin with, let us recall that simple is a natural number greater than zero that is only divisible by itself and one (“1” is not prime).
If there are more than two divisors, the number is considered composite, and it can be decomposed into a product of prime factors. This process is called factorization, consists of the following steps:
- We make sure that the given number is not prime. If it is up to 1000, then the table presented in a separate one can help us with this.
- We sort through all the prime numbers (from the smallest) in order to find the divisor.
- We perform the division, and for the resulting quotient we do the step above. If necessary, repeat this action several times until we get a prime number as a result.
Factorization examples
Example 1
Let’s decompose 63 into prime factors.
Decision:
- The given number is composite, so you can factorize.
- The smallest prime divisor is three. The quotient of 63 divided by 3 is 21.
- The number 21 is also divisible by 3, resulting in 7.
- Seven is a prime number, so we stop at it.
Typically, the factorization looks like this:
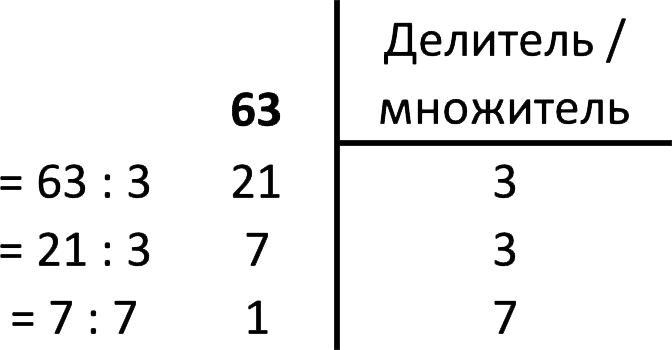
Answer: 63 = 3 3 7.
Example 2

Example 3