Contents
In this publication, we will consider the definition and main properties of the midlines of a convex quadrilateral regarding their intersection point, relationship with diagonals, etc.
Note: In what follows, we will consider only a convex figure.
Determination of the midline of a quadrilateral
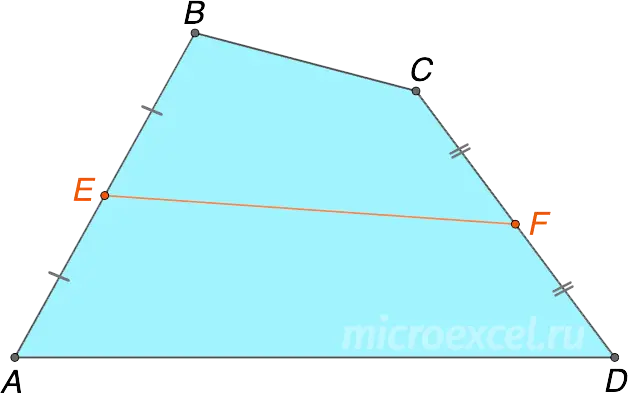
The segment connecting the midpoints of the opposite sides of the quadrilateral (i.e. not intersecting them) is called its middle line.
- EF – middle line connecting the midpoints AB и CD; AE=EB, CF=FD.
- GH – median line separating the midpoints BC и AD; BG=GC, AH=HD.
Properties of the midline of a quadrilateral
Property 1
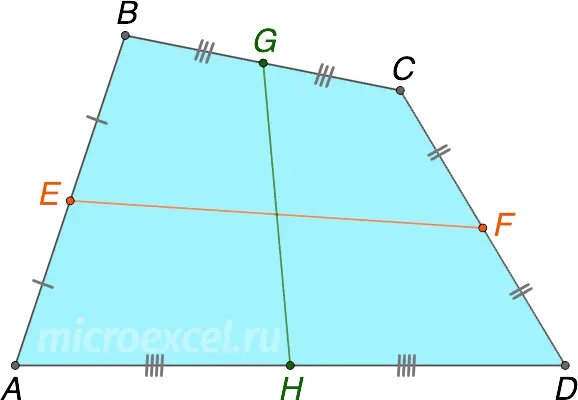
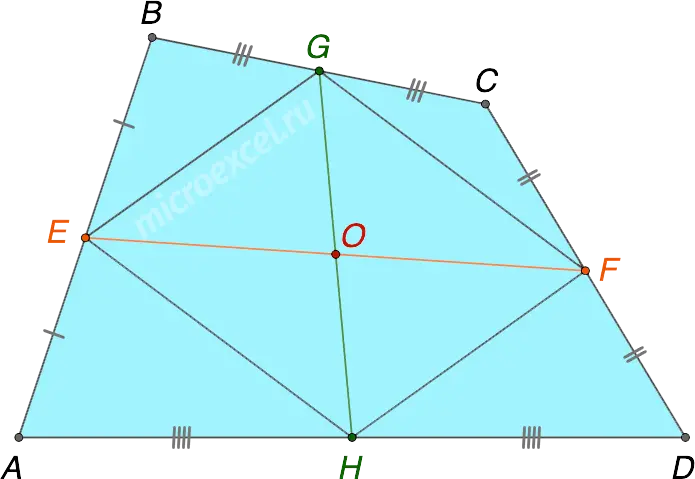
The middle lines of the quadrilateral intersect and bisect at the point of intersection.
- EF и GH (middle lines) intersect at a point O;
- EO=OF, GO=OH.
Note: Point O is centroid (or barycenter) quadrilateral.
Property 2
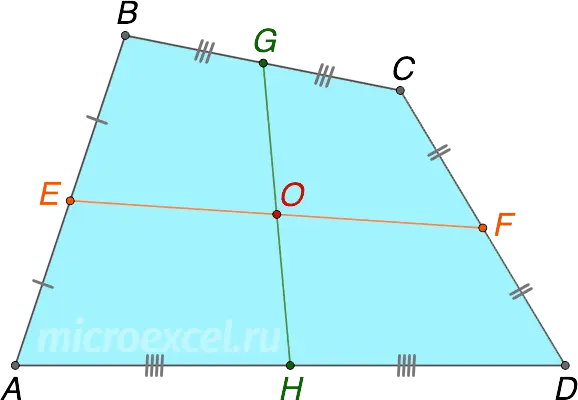
The point of intersection of the midlines of the quadrilateral is the midpoint of the segment connecting the midpoints of its diagonals.
- K – the middle of the diagonal AC;
- L – the middle of the diagonal BD;
- KL passes through a point O, connecting K и L.
Property 3
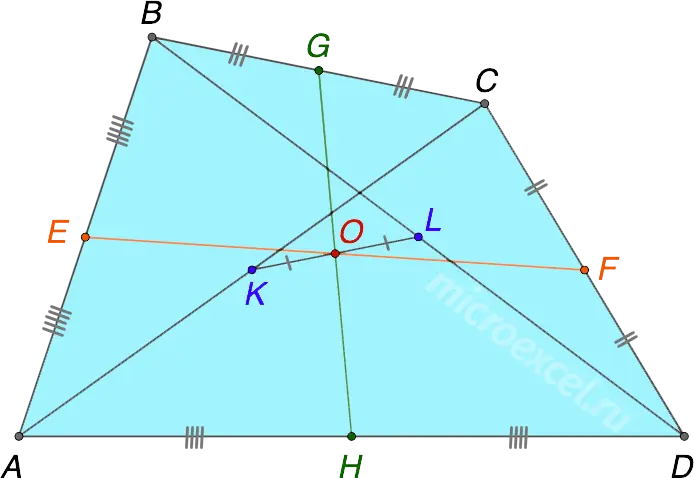
The midpoints of the sides of a quadrilateral are the vertices of a parallelogram called Parallelogram of Varignon.
The center of the parallelogram formed in this way and the point of intersection of its diagonals is the midpoint of the midlines of the original quadrilateral, i.e. their point of intersection O.
Note: The area of a parallelogram is half the area of a quadrilateral.
Property 4
If the angles between the diagonals of a quadrilateral and its midline are equal, then the diagonals have the same length.
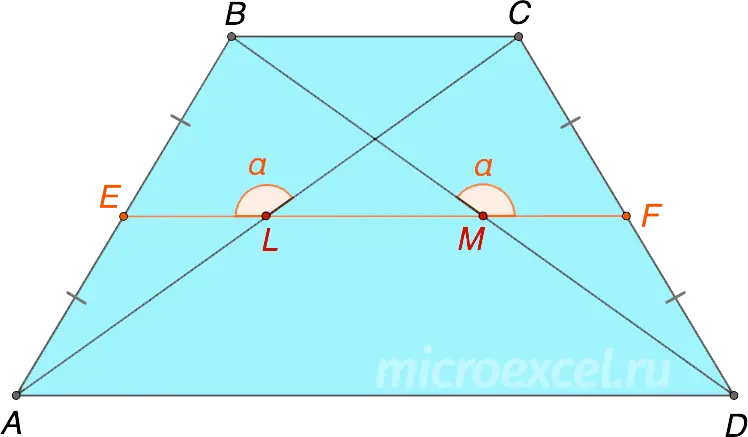
- EF – middle line;
- AC и BD – diagonals;
- ∠ELC = ∠BMF = a, Consequently AC=BD.
Property 5
The midline of a quadrilateral is less than or equal to half the sum of its non-intersecting sides (provided that these sides are parallel).
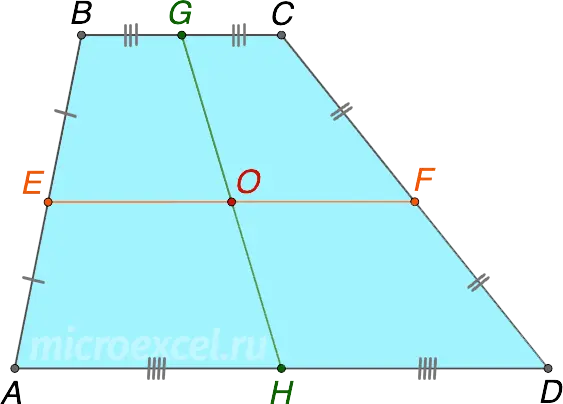
EF – a median line that does not intersect with the sides AD и BC.
In other words, the midline of a quadrilateral is equal to half the sum of the sides that do not intersect it if and only if the given quadrilateral is a trapezoid. In this case, the considered sides are the bases of the figure.
Property 6
For the midline vector of an arbitrary quadrilateral, the following equality holds:
![]()