Contents
In this publication, we will consider the definition, properties and sign of the middle line of a triangle, and also analyze an example of solving the problem for a better understanding of the theoretical material.
Definition of the midline of a triangle
The line segment that joins the midpoints of two sides of a triangle is called its middle line.

- KL – middle line of the triangle ABC
- K – middle side AB: AK = KB
- L – middle side BC: BL = LC
Properties of the midline of a triangle
Property 1
The median line of a triangle is parallel to one of its sides (which it does not intersect) and is half that side.
In the picture above:
- KL parallel AC
- KL = 1/2 ⋅ AC
Property 2
The middle line of the triangle cuts off from it (at a ratio of 1:2), the area of u4buXNUMXbwhich is XNUMX times less than the original one.
In the picture above:
- △KBL ∼ △ABC (similarity in proportionality of all sides)
- Hand △KBL two times smaller than the corresponding sides △ABC:
AB = 2KB, BC = 2BL, AC = 2KL
. - S△ABC = 4 ⋅ S△KBL
Property 3
In any triangle, three middle lines can be drawn.
KL, KM и ML – middle lines of a triangle ABC.
- KL || AC, KL = 1/2 ⋅ AC
- KM || BC, KM = 1/2 ⋅ BC
- ML || AB, ML = 1/2 ⋅ AB
Property 4
Three middle lines of a triangle divide it into 4 triangles of equal area.
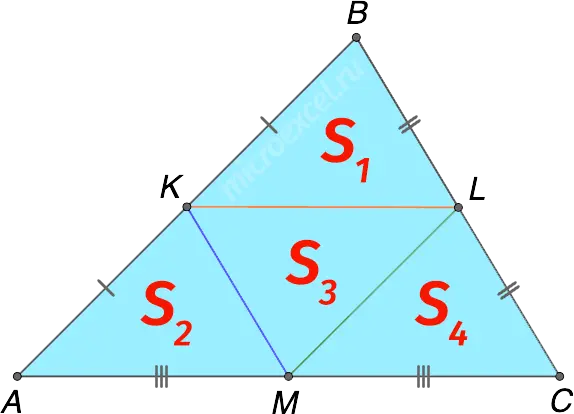
S1 = S2 = S3 = S4
Sign of the midline of a triangle
The segment passing through the midpoint of one of the sides of the triangle, intersecting the second and parallel to the third side, is the midline of this triangle.
Example of a problem
Given a triangle, two sides of which are 6 and 8 cm. Find the length of the midline connecting these sides.
Solution
A triangle with given sides is , and the known values are the lengths of the legs. The median line that connects the legs is parallel to the hypotenuse and equal to half its length.
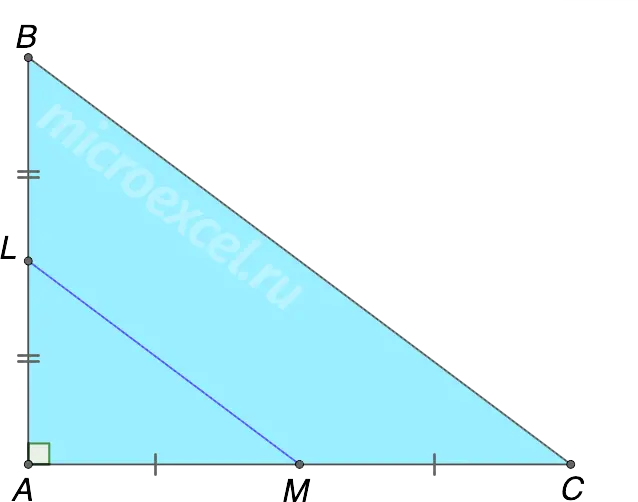
We can find the hypotenuse using .
BC2 =AB2 + AC2 = 62 + 82 = 100.
BC = 10.
So the middle line LM = 1/2 ⋅ BC = 1/2 ⋅ 10 = 5.









