Contents
In this publication, we will consider the definition, properties and sign of the midline of a trapezoid, and also analyze an example of solving the problem for a better understanding of the material presented.
Determining the midline of a trapezoid
The segment connecting the midpoints of the sides of a trapezoid is called its middle line.
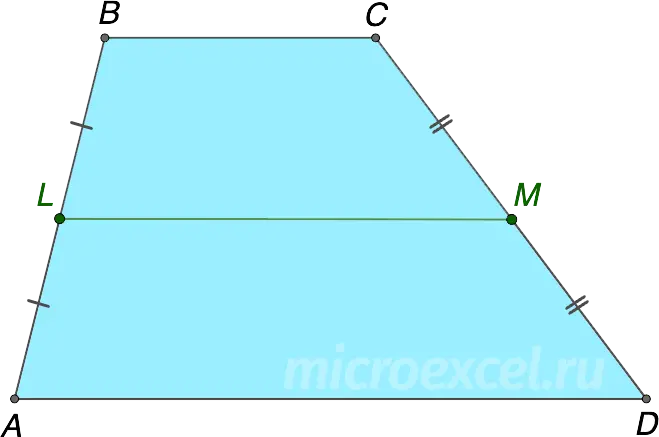
- LM – middle line of the trapezium ABCD
- L – middle side ABIe AL = LB
- M – middle side CDIe CM = MD
Properties of the midline of a trapezoid
Property 1
The midline of a trapezoid is parallel to its bases and equals their half sum.
For the picture above:
![]()
Property 2
The midline of a trapezoid bisects any segment whose ends lie on the bases of the given trapezoid.
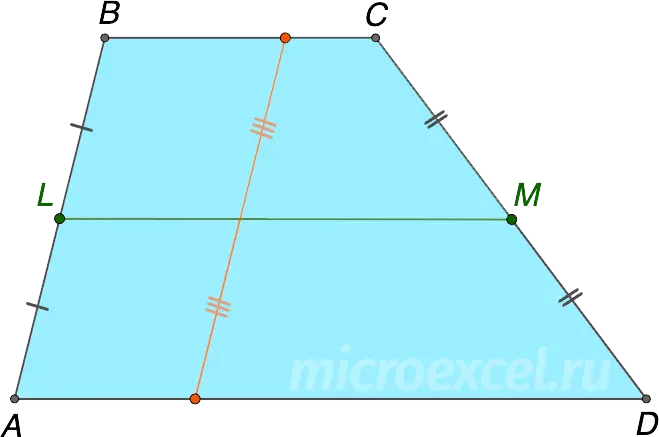
Property 3
The middle line of a trapezoid divides it into two other trapezoids, the areas of which are related as follows (see the first drawing of the publication):
![]()
![]()
![]()
Sign of the midline of the trapezium
If the segment coming out of the middle of the lateral side of the trapezoid intersects its second lateral side and, at the same time, is parallel to the bases of the figure, then it is the midline of this trapezoid.
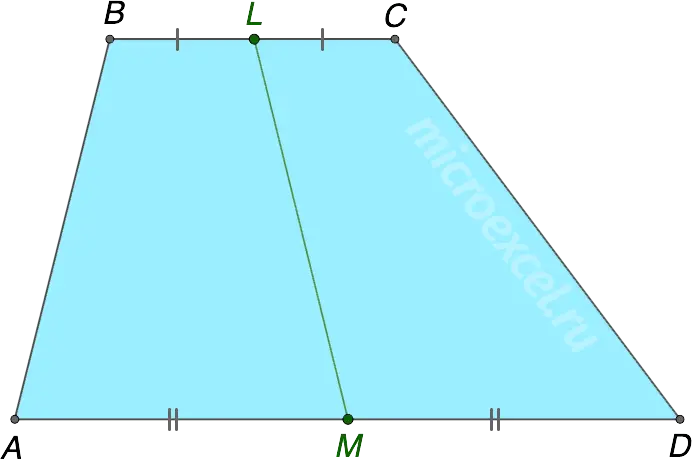
Second middle line
Sometimes additionally allocate second midline of the trapezoid is a segment that connects the midpoints of its bases. It should be remembered, however, that it does not apply Properties 1-3 и Signdiscussed above.
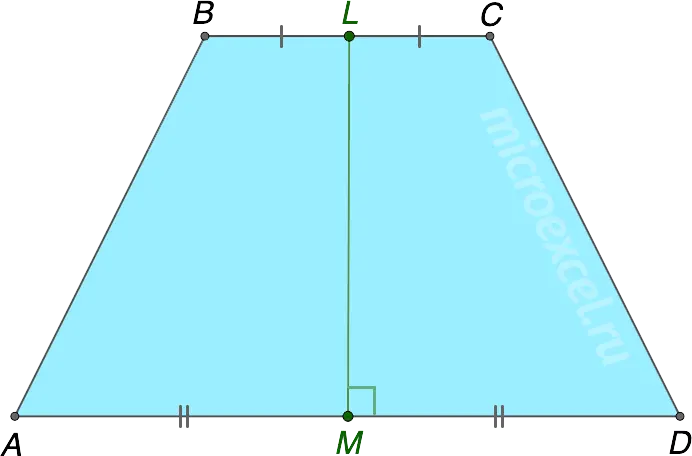
The second median line of an isosceles trapezoid is also its height.
Example of a problem
The median line of the trapezoid is 25 cm and its height is 7 cm. Find the area of the figure.
Solution
As we know, the area of a trapezoid is half the sum of the bases multiplied by the height. h: S = (a+b)/2 ⋅ h
In this case, half the sum of the bases is the middle line. Let’s denote it with the letter m. That is m = (a+b)/2.
In this way, S = m ⋅ h = 25 cm ⋅ 7 cm = 175 cm2.









