In this publication, we will consider the definition and main elements of a truncated cone. The presented information is accompanied by visual drawings for better perception.
Truncated Cone Definition
Truncated cone (conical layer) is a geometric figure in space; the part of a cone that remains between its base and a cutting plane parallel to that base.
Note: Within the framework of this publication, we will consider the most common type of truncated cone – straight circular.
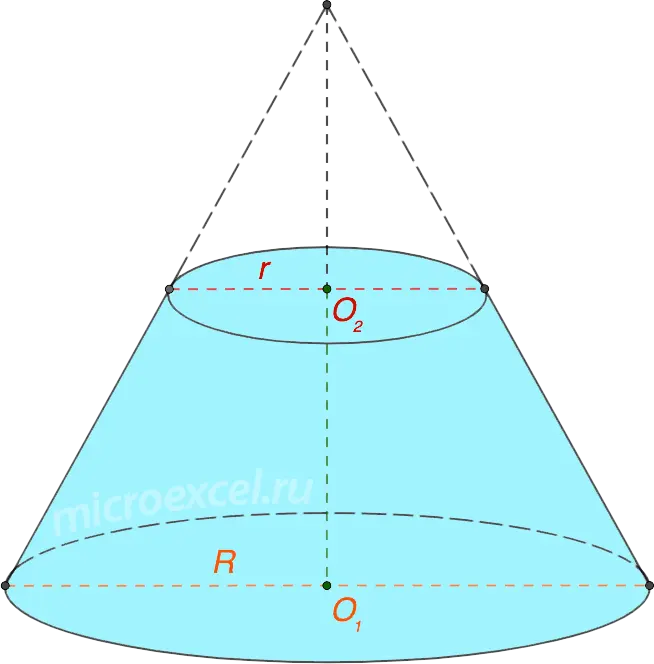
A truncated cone is formed by rotating a rectangular trapezoid through 360° around the side perpendicular to the base, or an isosceles trapezoid around its axis of symmetry by 180°.
In the figure below, the cone is formed by rotating an isosceles trapezoid ABCD around the axis O1O2.
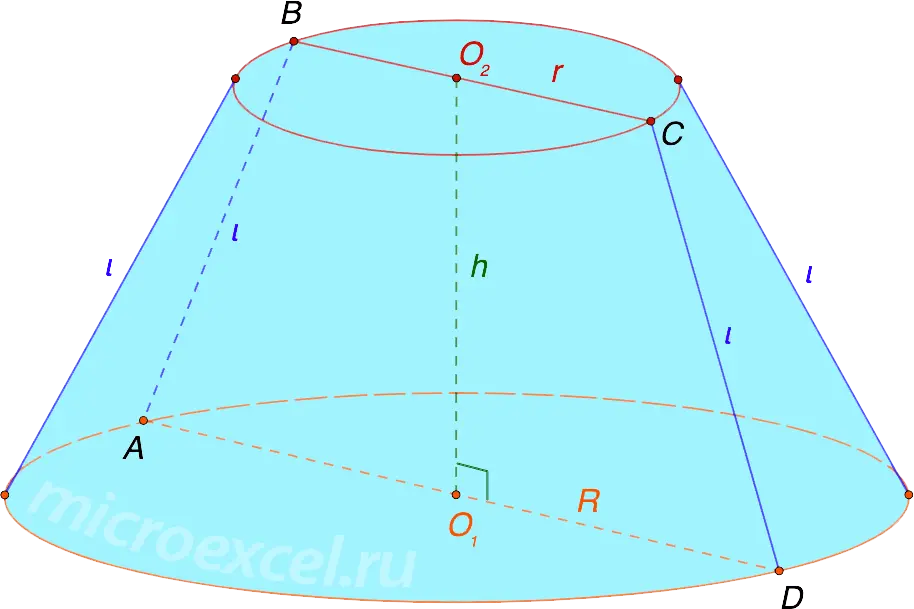
Basic elements of a truncated cone
- R – the radius of the larger base of the cone, which is a circle, with a center at a point O1 and diameter AD.
- r is the radius of the smaller base of the cone centered at the point O2, diameter – segment BC.
- h (O1O2) is the height of the cone; is also the height of the trapezoid ABCD and the axis of symmetry of both figures.
- l (AB, CD etc.) – generators of the cone; these are line segments connecting two points on the circles of its two bases (with the smallest possible distance). At the same time, they are the sides of the trapezoid (axial section of the cone).
- Axial section of a truncated cone is an isosceles trapezoid ABCD, formed as a result of the intersection of the cone by a plane passing through its axis.
- Truncated cone surface – the lateral surface and the surface of its two bases. Formulas for calculating , as well as a truncated cone are presented in separate publications.
Side surface development truncated cone looks like this:

The length of the larger (smaller) arc is equal to the circumference of the corresponding base of the cone (2πR or 2pr).









