Contents
In this publication, we will consider the definition, types and properties (regarding diagonals, angles, midline, intersection point of the sides, etc.) of one of the main geometric shapes – a trapezoid.
Definition of a trapezoid
Trapezium is a quadrilateral, two sides of which are parallel and the other two are not.
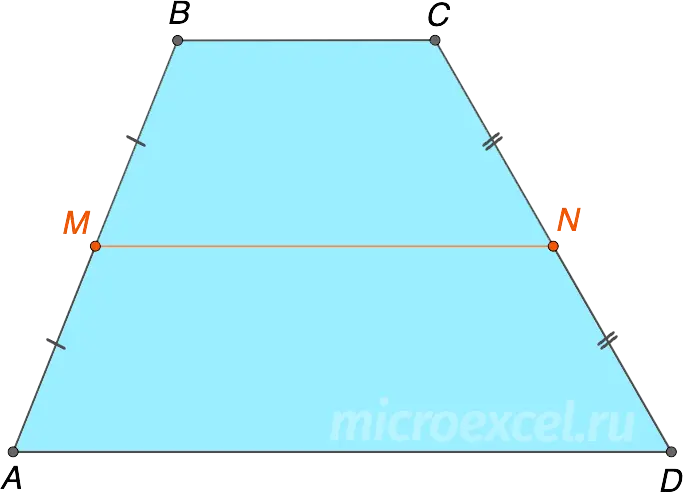
Parallel sides are called bases of a trapezoid (AD и BC), the other two sides side (AB и CD).
Angle at the base of the trapezoid – the internal angle of a trapezoid formed by its base and side, for example, α и β.
A trapezoid is written by listing its vertices, most often this is ABCD. And the bases are indicated by small Latin letters, for example, a и b.
Median line of the trapezoid (MN) – a segment connecting the midpoints of its lateral sides.
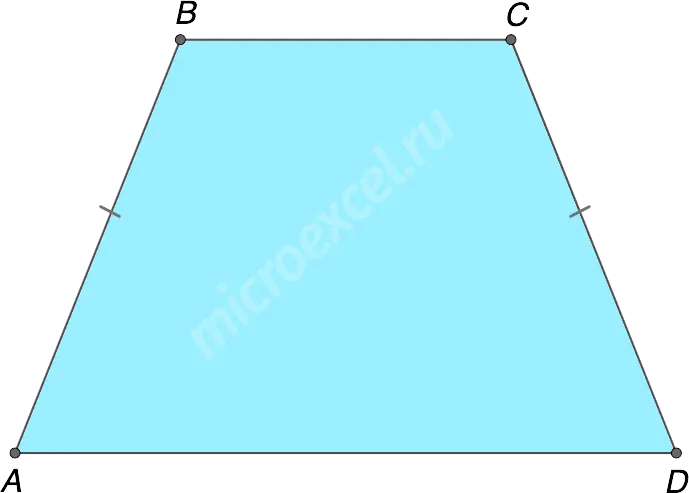
Trapeze Height (h or BK) is a perpendicular drawn from one base to another.

Types of trapezium
Isosceles trapezoid
A trapezoid whose sides are equal is called isosceles (or isosceles).

AB = CD
Rectangular trapezium
A trapezoid, in which both angles at one of its lateral sides are straight, is called rectangular.
∠BAD = ∠ABC = 90°
Versatile trapezoid
A trapezoid is scalene if its sides are not equal and none of the base angles are right.
Trapezoidal Properties
The properties listed below apply to any type of trapezoid. Properties and trapezoids are presented on our website in separate publications.
Property 1
The sum of the angles of a trapezoid adjacent to the same side is 180°.
α + β = 180°
Property 2
The midline of a trapezoid is parallel to its bases and equals half of their sum.

![]()
Property 3
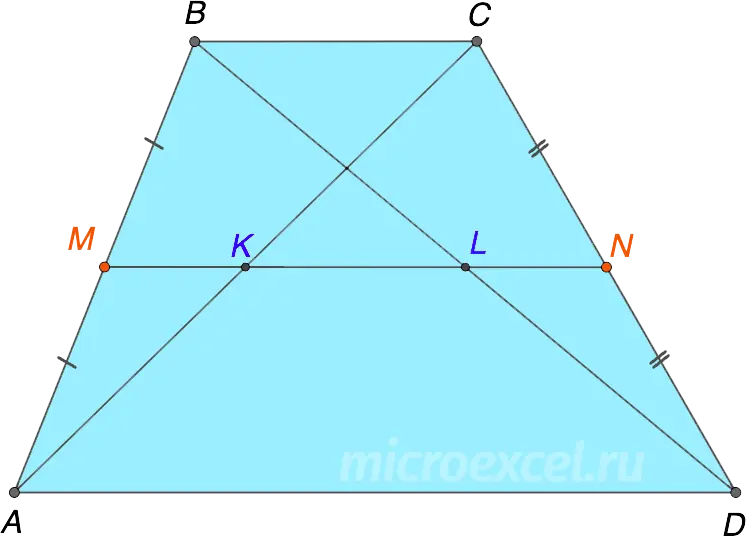
The segment that connects the midpoints of the diagonals of a trapezoid lies on its midline and is equal to half the difference of the bases.
![]()
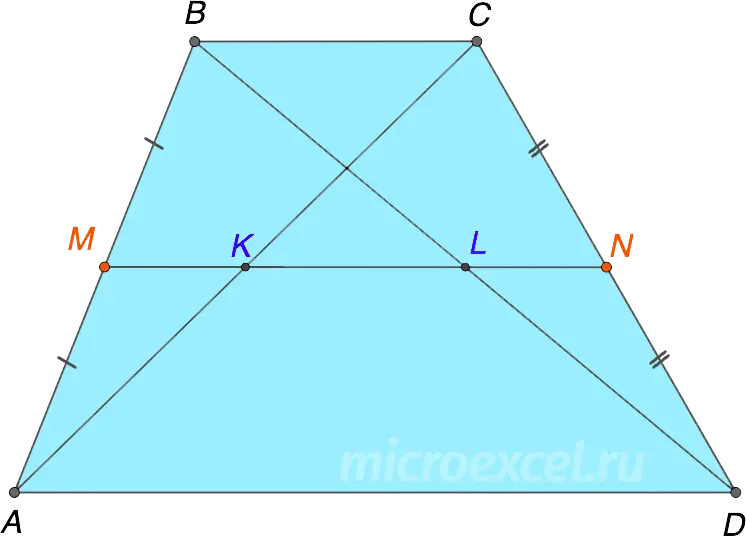
- KL a line segment that joins the midpoints of the diagonals AC и BD
- KL lies on the midline of the trapezium MN
Property 4
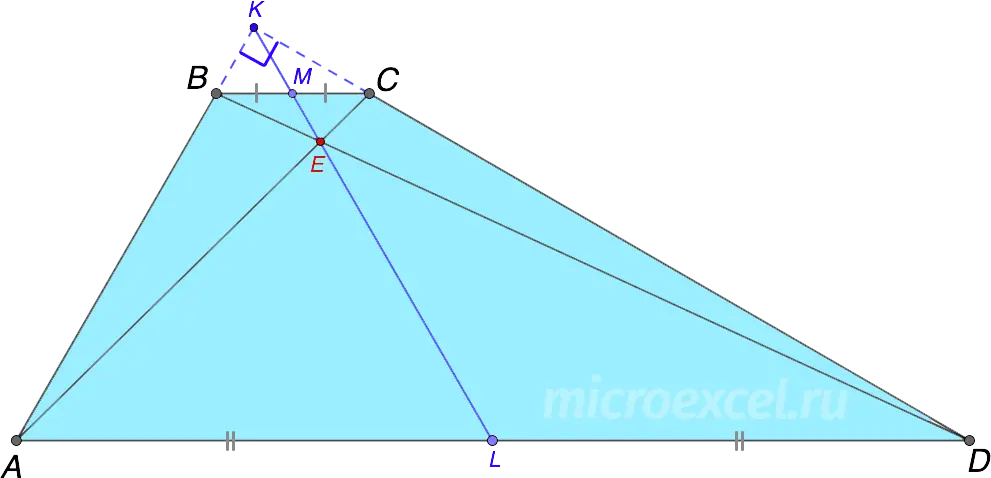
The points of intersection of the diagonals of the trapezoid, the extensions of its sides and the midpoints of the bases lie on the same straight line.
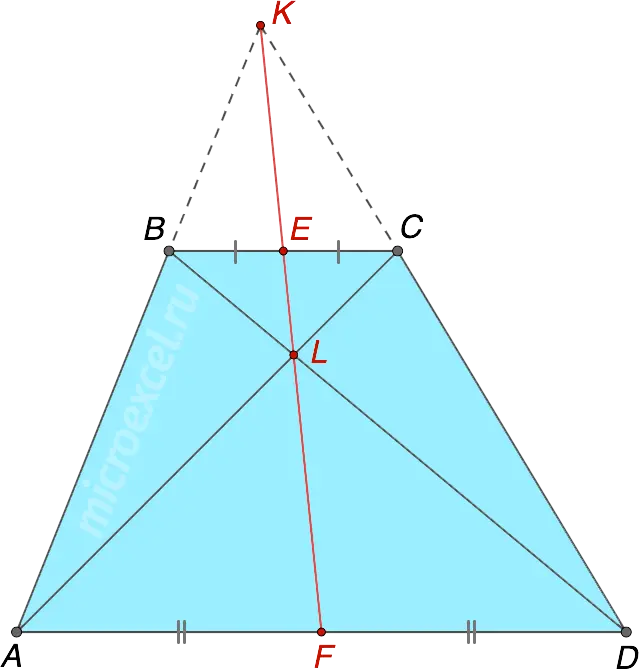
- DK – continuation of the side CD
- AK – continuation of the side AB
- E – middle of base BCIe BE = EC
- F – middle of base ADIe AF = FD
If the sum of the angles at one base is 90° (i.e. ∠DAB + ∠ADC u90d XNUMX °), which means that the extensions of the sides of the trapezoid intersect at a right angle, and the segment that connects the midpoints of the bases (ML) is equal to half of their difference.
![]()
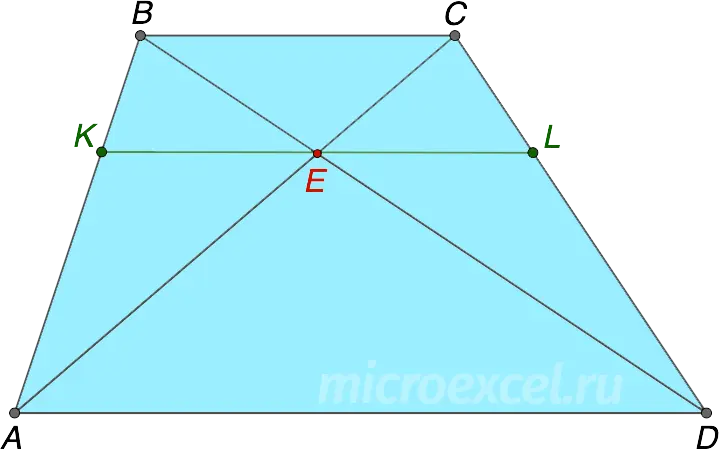
Property 5
The diagonals of a trapezoid divide it into 4 triangles, two of which (at the bases), and the other two (at the sides) are equal in .

- ΔAED ~ ΔBEC
- SΔABE = SΔCED
Property 6
A segment passing through the intersection point of the diagonals of a trapezoid parallel to its bases can be expressed in terms of the lengths of the bases:
![]()
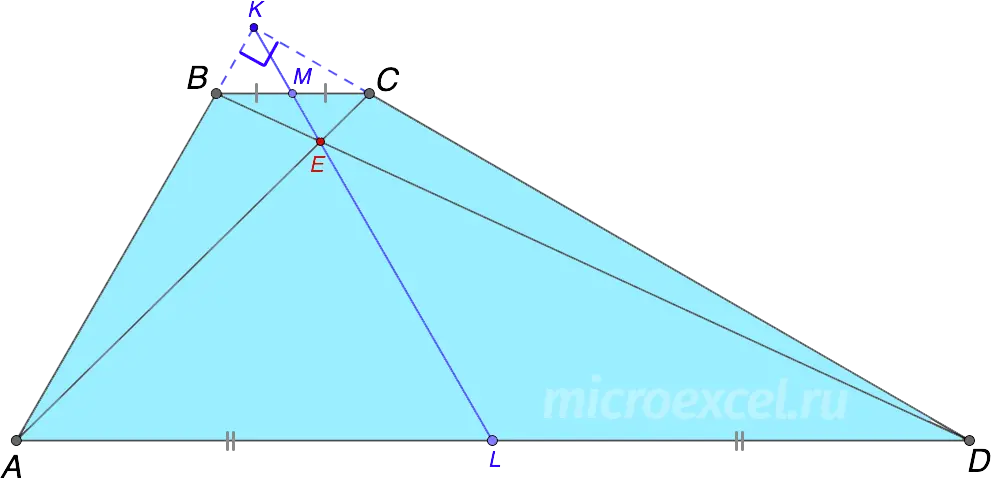
Property 7
The bisectors of the angles of a trapezoid with the same lateral side are mutually perpendicular.
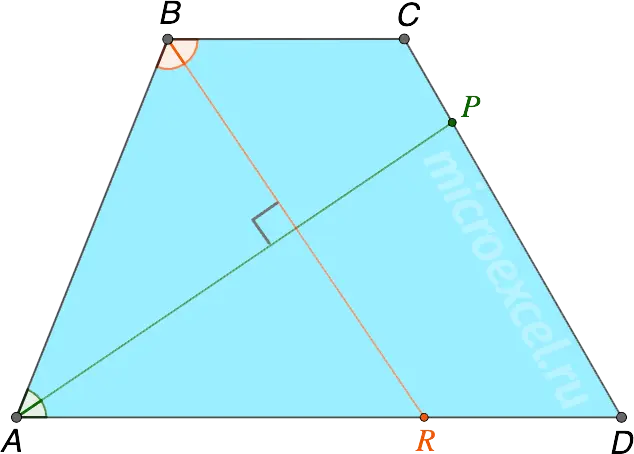
- AP – bisector ∠BAD
- BR – bisector ∠ABC
- AP perpendicular BR
Property 8
A circle can only be inscribed in a trapezoid if the sum of the lengths of its bases is equal to the sum of the lengths of its sides.
Those. AD + BC = AB + CD
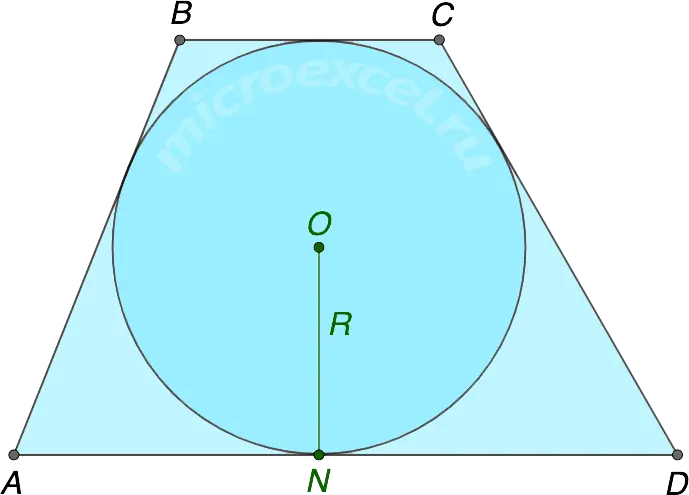
The radius of a circle inscribed in a trapezoid is equal to half its height: R = h/2.









