In this publication, we will consider what a straight line (on a plane) is, list its main properties, and also give options for the relative position of two straight lines.
Content
Line definition
Straight is a non-curving line that has neither beginning nor end. It is usually denoted in two generally accepted ways:
- Small Latin letter (a, b, c etc.)

- Two capital Latin letters, which are the names of the points through which the line passes.
 These points form a line AB, which is part of a line.
These points form a line AB, which is part of a line.
Mutual arrangement of lines
If we consider two straight lines on a plane, then they can be located in different ways in relation to each other:
- Parallel lines – do not intersect, therefore, they have no common points. Parallelism in geometry is indicated by two vertical lines. In our case, it is written like this:
AB || CD. 
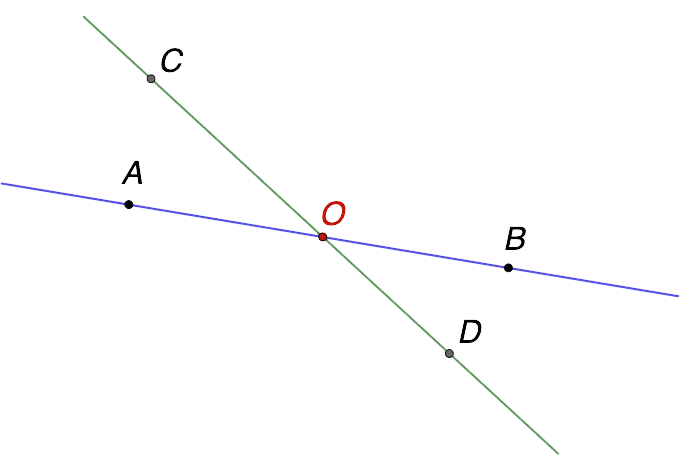
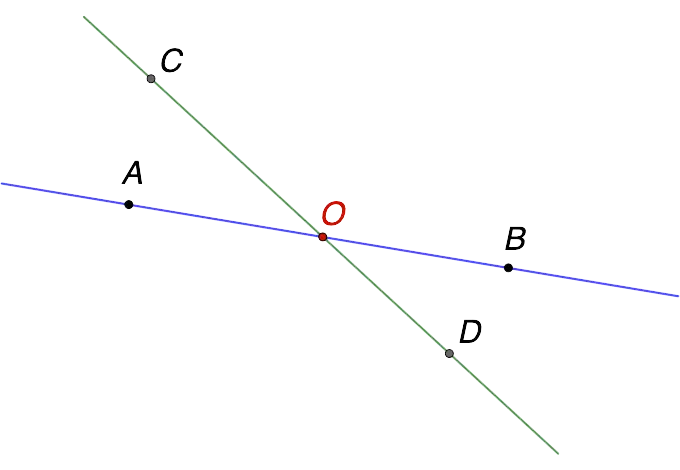
- intersecting lines – as the name implies, the lines intersect and have one common point (in the figure below, this is point O).

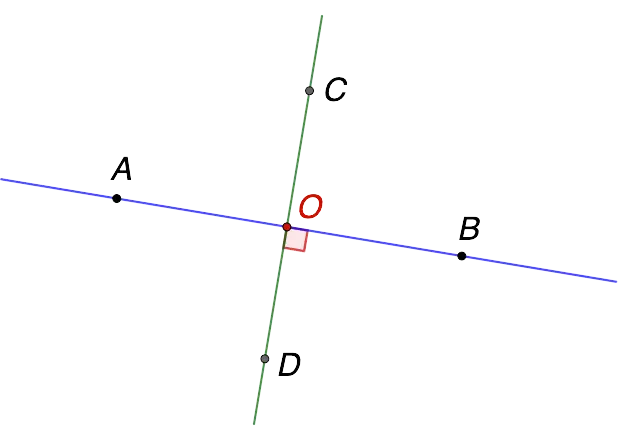
- Perpendicular lines – intersect at a right angle (90 degrees). The perpendicularity of lines is indicated by a special symbol – ⊥. That is, we write like this:
AB ⊥ CD. 
Note: in three-dimensional space, straight lines can be intersecting, i.e. lying in different planes.
Straight line properties
- An infinite number of lines can be drawn through any point.

- Through any two points that do not coincide, you can draw a straight line, and only one.
- Two lines on a plane are either parallel or intersecting (including perpendicular).
- If any two points of a line lie on a certain plane, then all points of this line belong to the same plane.










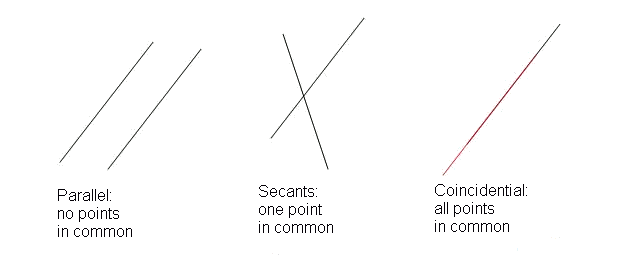

 These points form a line AB, which is part of a line.
These points form a line AB, which is part of a line.