What is a square trinomial: definition, formula, graph, examples

In this publication, we will consider what a square trinomial is, as well as give its formula and analyze the algorithm for constructing a graph (parabola). The presented information is accompanied by practical examples for better understanding.

Definition and formula of a square trinomial

Square trinomial is a polynomial of the form ax² + bx + c, where:

• x – variable;
• a, b и c – constant coefficients (senior, average and free, respectively);
• a ≠ 0.

examples:

• x² +7x +3
• 2x² – 9x + 6
• -5x² +11x +2

Square Trinomial Plot

The function of a square trinomial is called quadratic, and its graph is a parable. In order to construct it, you need to solve the quadratic equation ax² + bx + c = 0, which is obtained by adding an equal sign and zero at the end of the expression. We examined in detail finding the roots of an equation in a separate .

The chart has a vertex:

• maximum at a < 0;
• minimum at a > 0.

To make it clearer, we will analyze the algorithm for constructing a parabola using practical examples.

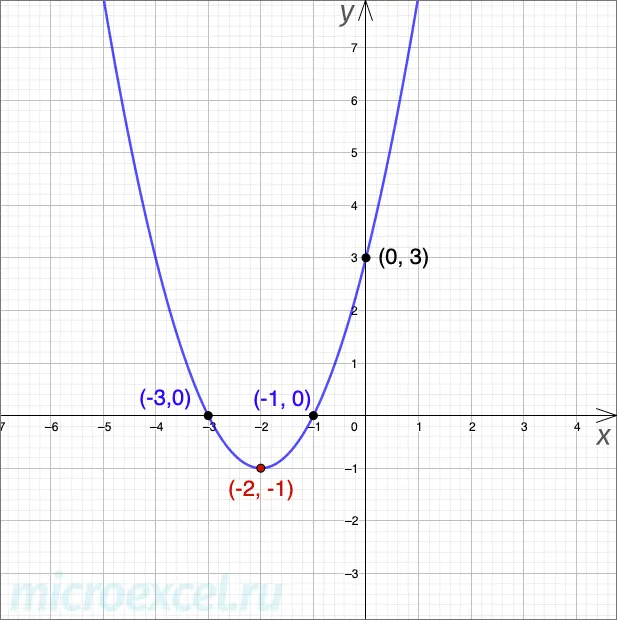
Example 1

Let’s plot a square trinomial x² + 4x + 3.

Solution

Equation roots x² + 4x + 3 = 0 are -3 and -1. Those. y takes on zero values ​​at xequal to these two numbers. In other words, the graph crosses the x-axis (Ox) at points (-3) и (-1).

Top of the parabola calculated by the formula ^-b/_2a. Since the coefficient a – a positive number, therefore, it will be its minimum.

I am. = ^-4/_{(2 ⋅ 1)} =-2

The resulting number is the valuex, now we substitute it into our formula and find y:

y = (-2)² + 4 (-2) + 3 = -1

So the vertex has coordinates (-2, -1).

It remains only to find at what point the graph intersects the y-axis (0y). To do this, in the trinomial formula, instead of x substitute the number 0:

y = (-0)² – 4 ⋅ 0 + 3 = 3

Therefore, it is a point with coordinates (0, 3).

Now we have all the necessary data to build a graph.

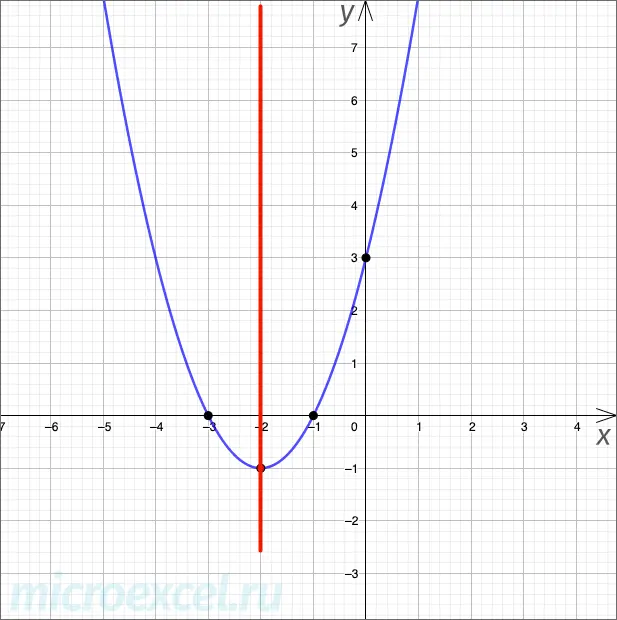
Note: Please note that the parabola is a symmetrical graph, i.e. if you draw a vertical line through its top, then the right side will be a mirror image of the left (and vice versa).

Example 2

I construct a parabola of three elements 3x² – 6x + 3.

Solution

The equation 3x² – 6x + 3 = 0 has only one root (x = 1). Therefore, the graph does not intersect, but touches the x-axis at the point (1, 0), which is also the minimum of the parabola (because the coefficient a – positive). We check:

I am. = ⁶/_{(2 ⋅ 3)} = 1 (this value x)

y = 3 ⋅ (1)² – 6 ⋅ 1 + 3 = 0

Now we find at what point the graph crosses the axis Oy, substituting in the formula instead of x number 0:

y = 3 ⋅ (0)² – 6 ⋅ 0 + 3 = 3

So the point of intersection with the y-axis is (0, 3).

We build a parabola taking into account the found points:

Example 3

And this is the graph of a quadratic function y = -2x² + 5x -2:

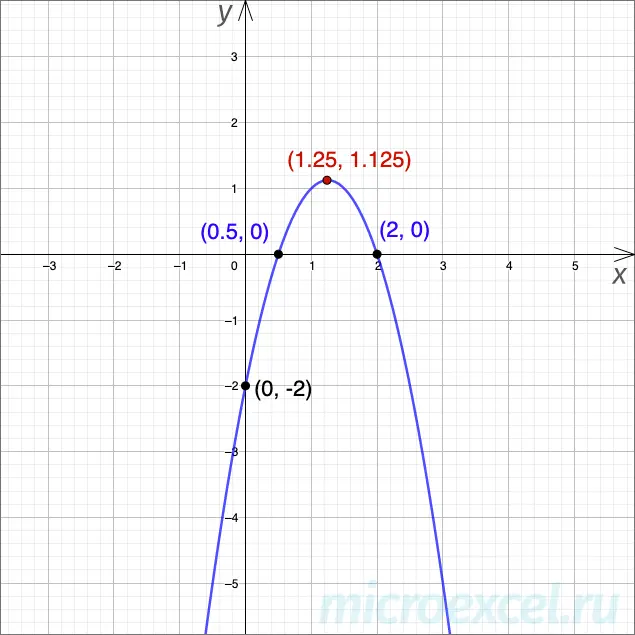
• Intersection points with the axis Ox: (0.5, 0) и (2, 0).
• As a is a negative number, then the maximum is reached at the point (1.25, 1.125).
• Axis intersection Oy – at the point (0, -2).