Contents
In this publication, we will consider the definition and properties (with pictures) of one of the main geometric shapes – a square.
A square is a shape that is a special case of a rectangle, which is why you can see the similarity of some algorithms. The calculation method always depends on the source data. To find out the area of a square, you need to know special formulas, consider five of them.
Definition of the square
Square is a regular geometric figure on a plane, which has four equal sides and right angles (ie 90°). Most often, a square is denoted by the names of vertices (for example, ABCD), and its side – in a small Latin letter (for example, a).

- AB = BC = CD = AD = a
- ∠ABC = ∠BCD = ∠ADC = ∠BAD = 90°
Square Properties
Property 1
The diagonals of the square are equal, located at right angles to each other, at the point of intersection they are divided in half.
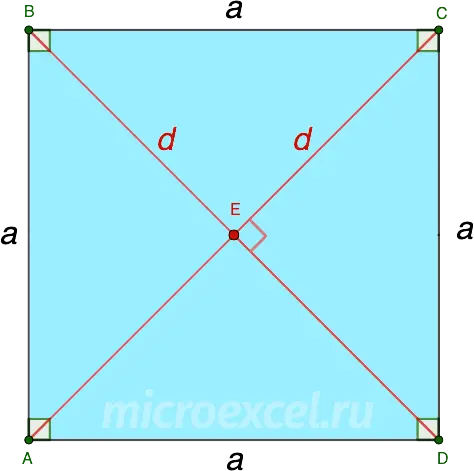
- AC = BD = d (diagonal)
- AE = EC = BE = ED
- ∠AEB = ∠AED = ∠BEC = ∠CED = 90°
Property 2
The diagonals of a square are the bisectors of its corners. For the picture above:
- BD – angle bisector ABC и ADC, Consequently, ∠ABD = ∠DBC = ∠ADB = ∠BDC
- AC – angle bisector BAD и BCD, Consequently, ∠BAC = ∠CAD = ∠BCA = ∠ACD
Property 3
The center of the circles described around and inscribed in the square is the point of intersection of its diagonals (in our case – E).
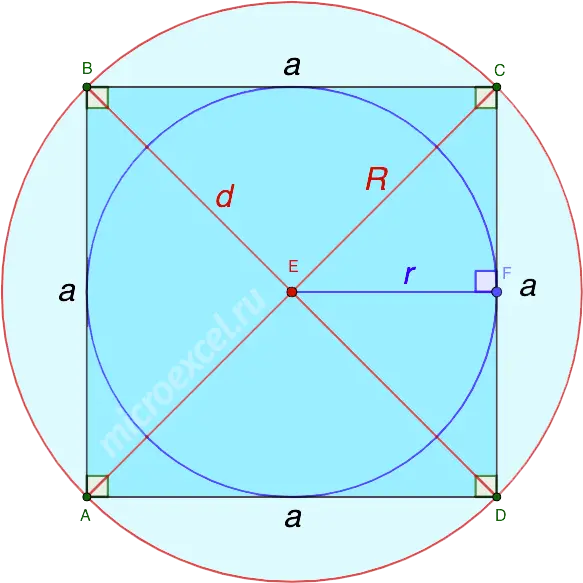
In this case, the radii of circles can be calculated through the length of the side or diagonal of the square:
![]()
![]()
Here:
- R is the radius of the circumscribed circle;
- r is the radius of the inscribed circle;
- a is the length of the side of the square;
- d is the length of the diagonal of the square.
Also, one radius can be expressed in terms of another:
![]()
Property 4
Knowing the length of a side or diagonal of a square, you can find its area or perimeter.
Perimeter (P) of the square across the side:
P = a + a + a + a = 4 ⋅ a
Perimeter (P) of the square through the diagonal:
![]()
Area (S) of the square across the side:
P = a ⋅ a = a2
Area (S) of the square through the diagonal:
![]()
How to determine the area of a square
A square is a shape that is a special case of a rectangle, which is why you can see the similarity of some algorithms. The calculation method always depends on the source data. To find out the area of a square, you need to know special formulas, consider five of them.
If the length of a side is known
We multiply it by the same number or square it.
S = a × a = a2, where S is the area, a is the side.
This formula is passed in the 3rd grade. Third-graders do not need to know the remaining formulas yet, but they will be useful to students in grade 8.
If we are given a diagonal
We square it and divide by two.
S = d2 : 2, where d is the diagonal.
If the radius of the inscribed circle is known
We multiply its square by four.
S = 4 × r2, where r is the radius of the inscribed circle.
If we have the radius of the circumscribed circle
Let’s square it and multiply it by two.
S = 2 × R2, where R is the radius of the circumscribed circle.
If there is a perimeter
We have to square it and divide by 16.
S = Р2 : 16, where P is the perimeter.
The perimeter of any quadrilateral is equal to the sum of the lengths of all its sides.
Important!
The problem cannot be solved if the length and width are given in different units. For the right decision, translate all the data to one unit of measure, and everything will work out.Popular area units:
square millimeter ( mm 2 );
square centimeter ( cm 2 );
square decimeter ( dm 2 );
square meter ( m 2 );
square kilometer ( km2 ) ;
hectare (ha).
https://www.youtube.com/watch?v=lAJCEzueXV0
S square. Problem solving
We have analyzed five formulas for calculating the area of a square. Now let’s practice!
Task 1. How to find the area of a square whose diagonal is 90 mm.
How do we decide:
Let’s use the formula: S = d 2 : 2.
Substitute the value of the diagonal into the formula: S = 90 2 : 2 = 4050 mm 2 .
Answer: 4050 mm 2 .
Task 2. A circle is inscribed in a square. Find the area of the square if the radius of the circle is 24 cm.
How do we decide:
If a circle is inscribed in a square, then the side of the square is equal to the diameter:
a = d
The diameter of a circle is equal to two radii:
d = 2r
It turns out that the side is equal to two radii:
a = 2r
We use the formula for finding the area of a square through the side:
S \u003d a 2
Since from point 3 we got that the side is equal to two radii, then the square area formula will take the form:
S \u003d (2r) 2
S \u003d 4r 2
Now let’s substitute the radius value into the area formula:
S \u003d 4 × 24 2 \u003d 2304 cm 2
Answer: 2304 cm 2 .
Источник – Онлайн школа Skysmart: https://skysmart.ru/articles/mathematic/ploshad-kvadrata









