Contents
In this publication, we will consider the definition, properties and features of one of the main geometric shapes – a rectangle. We also give formulas with which you can find its area and perimeter.
Definition of a rectangle
Rectangle is a quadrilateral in which all angles are equal to 90 ° (i.e., they are right).
∠ABC = ∠BCD = ∠BAD = ADC = 90°
The rectangle is made up of:
- lengths – a longer pair of sides. Usually denoted by a Latin letter, for example, a;
- width – a shorter pair of sides. Most often referred to as b.
The rectangle itself is usually written by listing its vertices, for example, ABCD in our case.
Note: Rectangle is a variant of .
Rectangle properties
Property 1
Opposite sides of a rectangle are pairwise parallel and equal.
- AD = BC = a, AD || BC
- AB = CD = b, AB || CD
Property 2
The length and width of the rectangle are both its heights, because they are mutually perpendicular.
- a is the height h1drawn to the side b
- b is the height h2drawn to the side a
Property 3
If you connect the midpoints of the sides of the rectangle, you get.
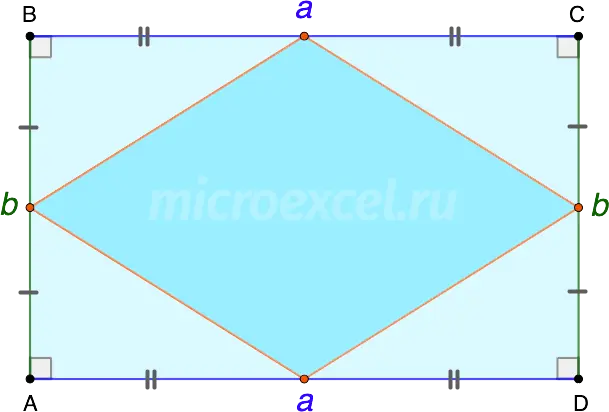
Property 4
Diagonal square (d) of a rectangle is equal to the sum of the squares of its adjacent sides.
d2 = A2 + b2
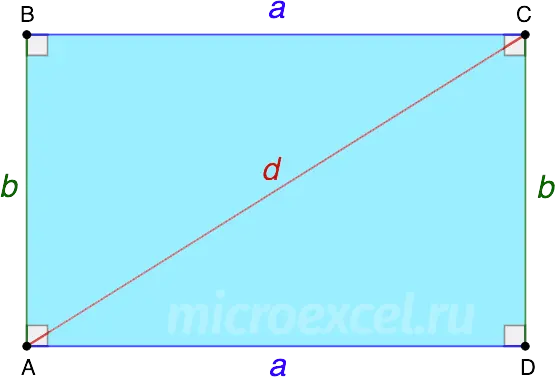
This follows from , which can be applied to any of the right triangles that result from dividing a rectangle by a diagonal.
Property 5
The diagonals of the rectangle are equal, and at the point of intersection they are divided in half.
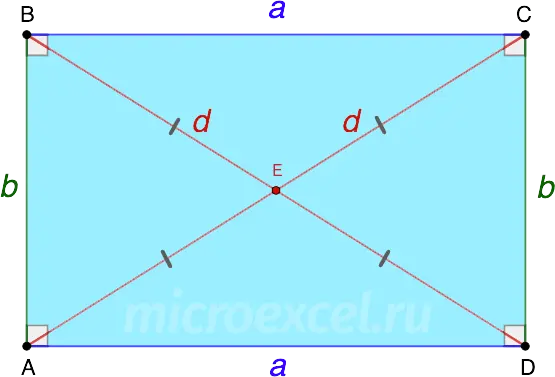
- AC = BD = d
- AE = EC = BE = ED
Property 6
Around any rectangle, you can describe a circle, radius (R) which is equal to half the diagonal of this rectangle.
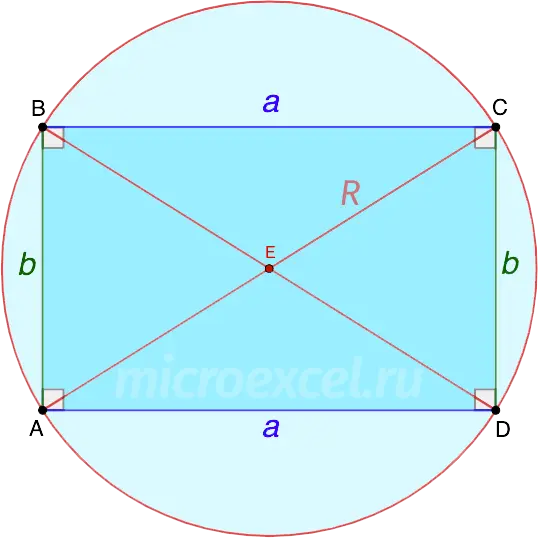
Therefore, the diameter of the circle is equal to the total length of the diagonal of the rectangle.
Rectangle Features
A parallelogram is a rectangle if one of the following is true:
- Its diagonals are equal.
- All its angles are equal.
- If the square of a diagonal is equal to the sum of the squares of its adjacent sides.
Formula
1. Area of a rectangle (S):
S = a ⋅ b
2. Rectangle Perimeter (P):
P = a + a + b + b = 2a + 2b