In this publication, we will consider what a broken line is in mathematics, how it is denoted, what elements it consists of, what types of it are, and we will also analyze an example of solving a problem on this topic.
Polyline definition
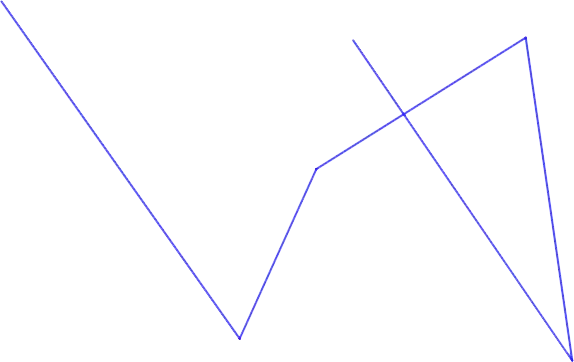
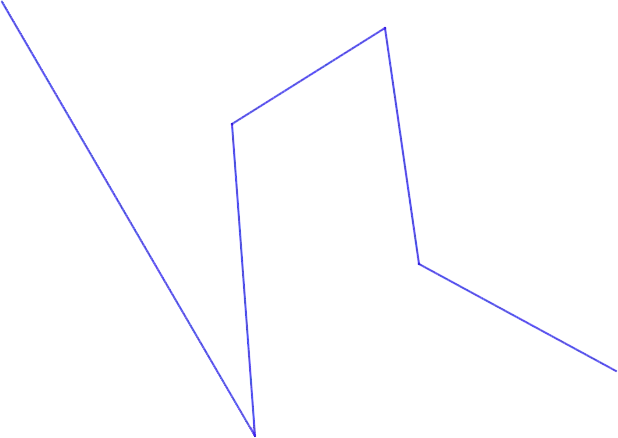
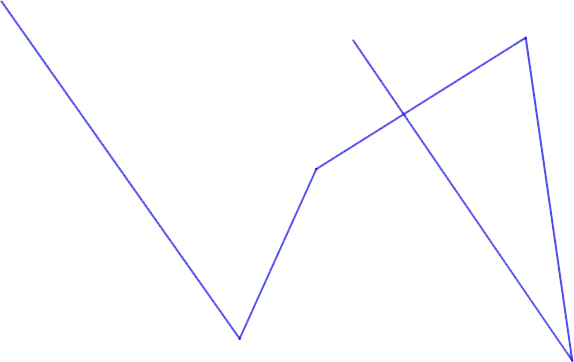
broken line – a line that consists of successively connected segments located at different angles (but not at 180 °).
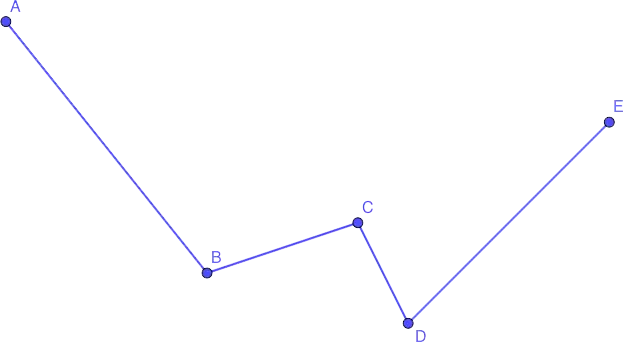
That is, if you “break” a long segment (in one or several places), you get a broken one.
Polyline elements:
- Links – segments that form a polyline (in the figure below, these are AB, BC, CD and DE). If the end of one link is the beginning of another, such links are called adjacent (AB and BC, BC and СD, CD and DE).

- Tops – all points on the polyline that are its beginning and end, as well as the points of connection of links (A, B, C, D and E).
A polyline is denoted by listing all its vertices in order, i.e. in our case – ABCDE.
Polyline length is equal to the sum of the lengths of all its links, i.e. ABCDE = AB + BC + CD + DE.
Types of broken line
- Without self-intersections – no link of the polyline intersects with another.

- Self-intersecting – at least two links of the polyline have a common point, not counting the common vertex.

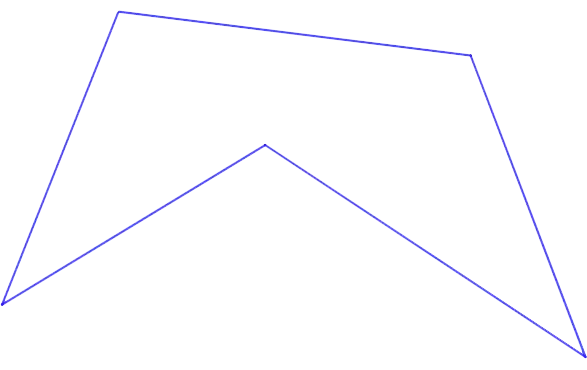
- Closed – the first and last points of the polyline coincide.

Example of a problem
A broken line is given, consisting of 5 links, the first of which is 7 cm, and each subsequent one is 3 cm longer than the previous one. Find the total length of the broken line.
Solution
First, let’s calculate the lengths of all the links:
- 2 links = 7 + 3 = 10 cm
- 3 links = 10 + 3 = 13 cm
- 4 links = 13 + 3 = 16 cm
- 5 links = 16 + 3 = 19 cm
Now it remains only to add all the obtained values to get the length of the polyline: 7 + 10 + 13 + 16 + 19 =