Contents
In this publication, we will consider the definition, properties and features (with drawings) of one of the main geometric shapes – a parallelogram.
Definition of a parallelogram
Parallelogram is a quadrilateral whose opposite sides are pairwise parallel.

AB || CD, BC || AD
A parallelogram is usually written by listing its four vertices, for example, ABCD. And pairs of parallel sides, most often, are indicated by small Latin letters, in our case – a и b.
Special cases of a parallelogram: , and .
Parallelogram Properties
Property 1
Opposite (or opposite) sides of a parallelogram are equal.

- AB = CD
- BC = AD
Property 2
Opposite angles of a parallelogram are equal.
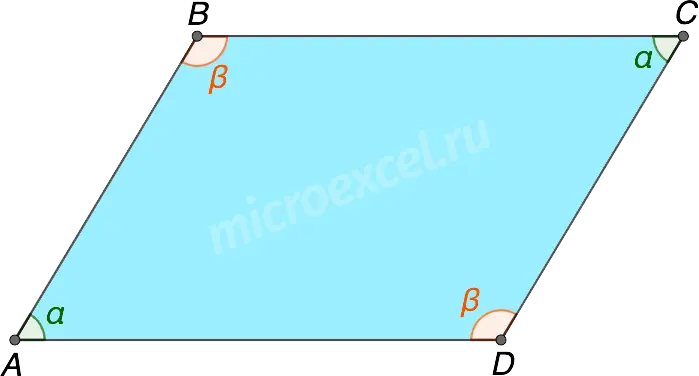
- ∠ABC = ∠ADC
- ∠BAD = ∠BCD
Property 3
The sum of the angles of a parallelogram adjacent to one side is 180°.
For the picture above: α + β = 180°.
Property 4
Any of the two diagonals of a parallelogram divides it into two equal triangles.
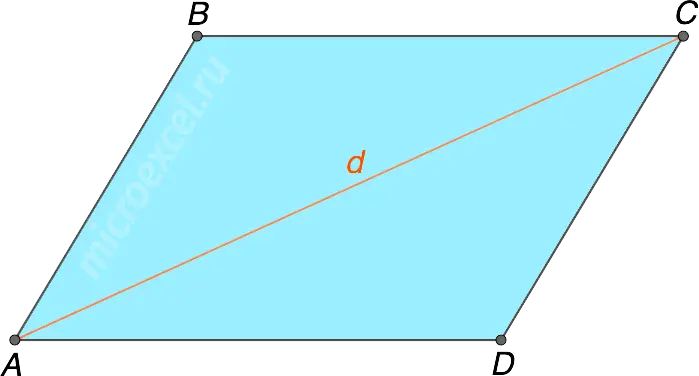
△ABC = △ADC
Property 5
The diagonals of a parallelogram at the point of intersection are bisected.
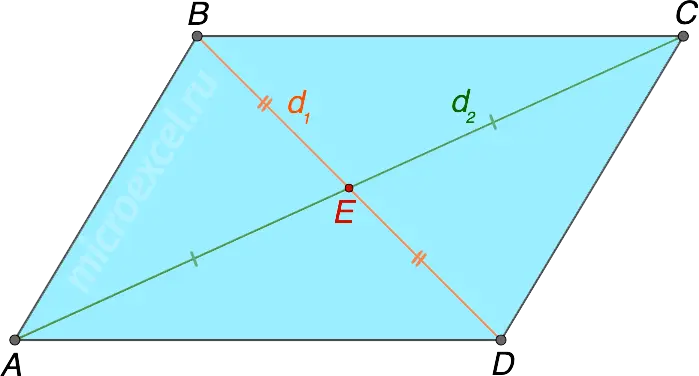
- AE = EC
- BE = ED
Property 6
The point of intersection of the diagonals of a parallelogram (also called the center of symmetry) is also the point of intersection of its midlines.
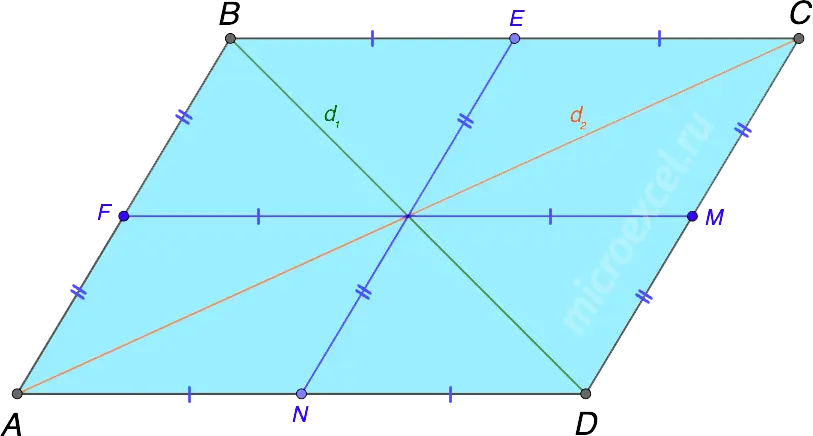
Middle line of the quadrilateral is a line segment that connects the midpoints of its opposite sides.
In this case, the middle lines are segments FM и EN.
Property 7
The angle between two heights in a parallelogram is equal to its acute angle.
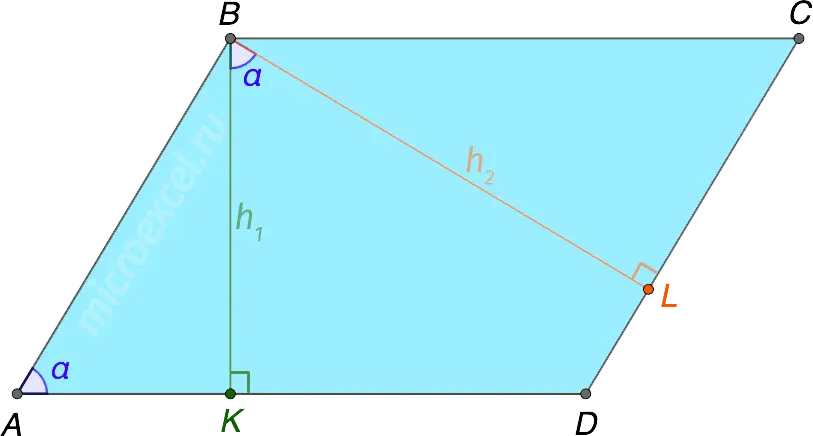
- BL – height drawn to the side CD
- BK – height driven to the side AD
- ∠KBL = ∠BAK
Property 8
The bisectors of the angles of a parallelogram adjacent to one side are mutually perpendicular (i.e., located at an angle of 90 ° to each other).
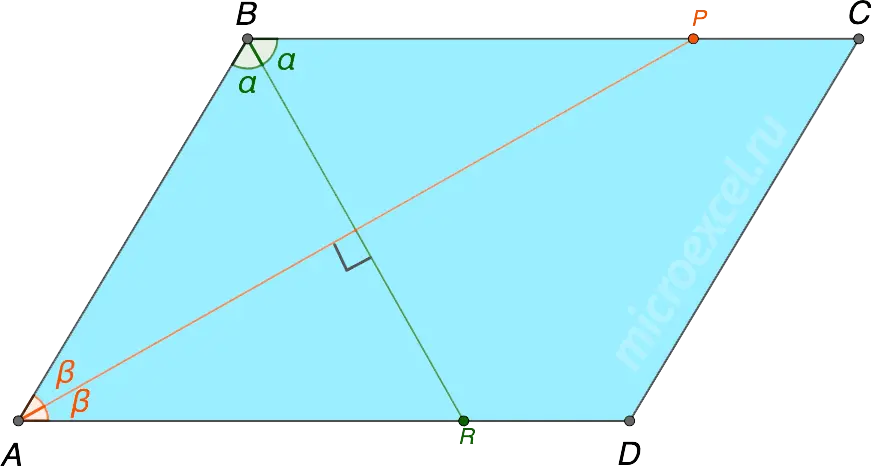
- AP – bisector ∠BAD
- BR – bisector ∠ABC
- AP perpendicular BR
Property 9
Bisectors of two opposite angles of a parallelogram are parallel.
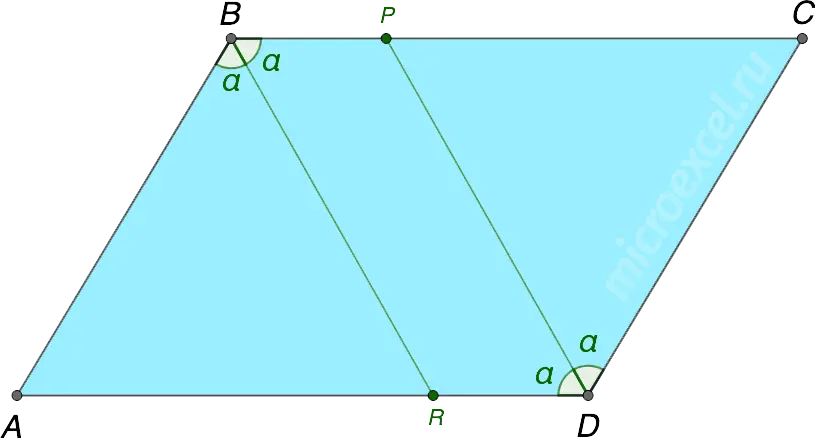
Corners ABC и ADC opposite. Their bisectors are parallel, i.e. BR || DP.
Property 10: parallelogram identity
The sum of the squares of the diagonals of a parallelogram is twice the sum of the squares of its adjacent sides.
![]()
Symptoms of a parallelogram
Quadrangle ABCD without self-intersections is a parallelogram if one of the following statements is true for it:
- Two opposite sides are both equal and parallel.
- All opposite angles are equal in pairs.
- All opposite sides are equal.
- All opposite sides are pairwise parallel.
- Both diagonals at the point of intersection are divided in half.










Эн сонун