What is a cube: definition, properties, formulas

In the publication, we will consider the definition and basic properties of a cube, as well as formulas related to this geometric figure (calculation of the surface area, perimeter of edges, volume, radius of the circumscribed / inscribed ball, etc.).

Definition cube

Cube is a regular polyhedron all of whose faces are squares.

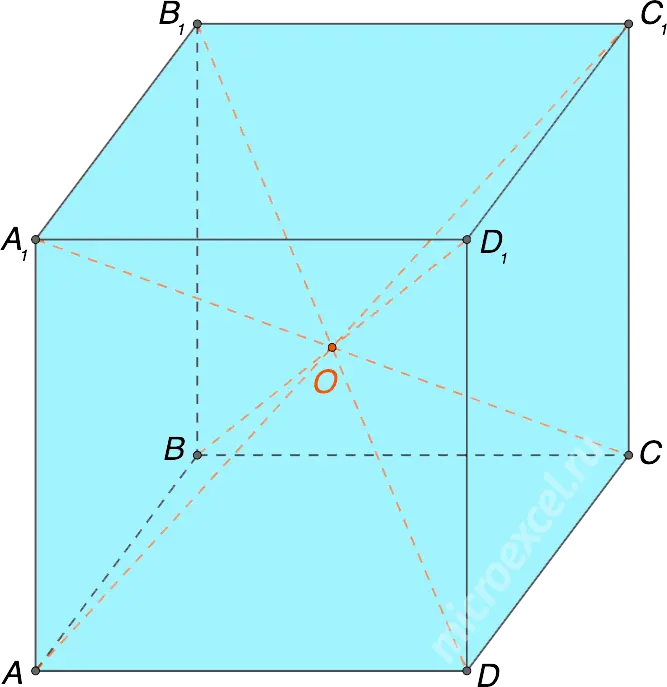
• Cube vertices are the points that are the vertices of its faces.

  There are 8 in total: A, B, C, D, A₁, B₁C₁ и D₁.

• Cube ribs are the sides of its faces.

  There are 12 in total: AB, BC, CD, AD, AA₁, BB₁, CC₁, DD₁, A₁B₁, B₁C₁C₁D₁ и A₁D₁.

• faces of a cube are the squares that make up the figure.

  There are 6 in total: ABCD, A₁B₁C₁D₁, AA₁B₁B, BB₁C₁C, CC₁D₁D и AA₁D₁D.

Note: the cube is a special case of or .

Cube properties

Property 1

As follows from the definition, all edges and faces of a cube are equal. Also, the opposite faces of the figure are pairwise parallel, i.e.:

• ABCD || A₁B₁C₁D₁
• AA₁B₁B || CC₁D₁D
• BB₁C₁C || AA₁D₁D

Property 2

The diagonals of the cube (there are only 4 of them) are equal and are divided in half at the point of intersection.

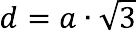
• AC₁ = BD₁ = A₁C = B₁D (diagonal cube).
• О – the point of intersection of the diagonals:

  AO = OC₁ = BO = OF₁ = A₁O = OC = B₁O = OD.

Property 3

All dihedral angles of a cube (the angles between two faces) are equal to 90°, i.e. are straight.

For example, in the figure above, the angle between the faces ABCD и AA₁B₁B is direct.

Cube formulas

We adopt the following notation, which will be used below:

• a – cube rib;
• d is the diagonal of a cube or its faces.

Diagonal

The length of the diagonal of a cube is equal to the length of its edge multiplied by the square root of three.

Face Diagonal

The diagonal of a cube’s face is equal to its edge times the square root of two.

Total surface area

The total surface area of ​​a cube is equal to six areas of its face. The formula can use the length of an edge or a diagonal.

Rib perimeter

The perimeter of a cube is equal to the length of its edge multiplied by 12. It can also be calculated in terms of the diagonal.

Volume

The volume of a cube is equal to the length of its edge cubed.

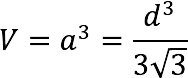
Radius of the circumscribed sphere

The radius of a sphere circumscribed about a cube is equal to half of its diagonal.

Inscribed ball radius

The radius of a sphere inscribed in a cube is equal to half the length of its edge.