What are complex numbers

In this publication, we will consider the definition of a complex number, its algebraic form and geometric interpretation, as well as the properties of arithmetic operations performed with such numbers.

Definition of a complex number

A complex number is a number of the form z = a + bi, where:

• a и b are real numbers;
• i is an imaginary unit for which the equality is true: i² =-1;
• a is the real part;
• bi is the imaginary part.

Note: a + bi is the algebraic form of a complex number, which should be taken as a whole, and not as an addition.

The set of complex numbers is represented by a symbol similar to the letter C.

If b = 0, then the complex number takes the form: z = a + 0 ⋅ i = a. Thus, a real (real) number is a special case of a complex number.

Geometric interpretation of complex numbers

Complex numbers can be transferred to the coordinate (complex) plane, the abscissa axis of which will be the real part (Re), and the y-axis is the imaginary (Im).

As an example, the following complex numbers are shown below, which can be interpreted as vectors:

• z=1+4i
• z = 2 – i
• z = -3 – 2i
• z = -3 + 2i
• z = 3
• z = -2i

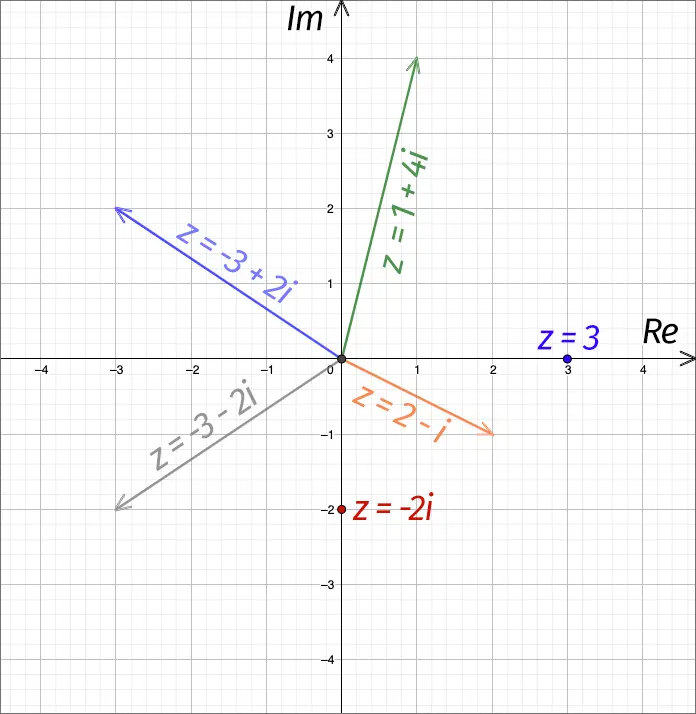
• z = 3 is a complex number with zero imaginary part, i.e. in fact it is a real number.
• z = -2i is an exclusively imaginary number with zero real part.

Arithmetic operations with complex numbers

Addition, subtraction, multiplication and division of complex numbers are performed according to the same laws that apply to ordinary numbers.

For example, the

(a + bi) + (c + di) = (a + c) + (b + d)i

(a + bi) – (c + di) = (a – c) + (b – d)i

Example 1: add two complex numbers: x = 2 + 4i и y = 1 – 3i.

Decision:

x + y = (2 + 4i) + (1 – 3i) = (2 + 1) + (4 – 3)i = 3 + i.

Example 2: subtract from complex number x = 6 – 2i number y = 3 + 5i.

Decision:

x – y = (6 – 2i) – (3 + 5i) = 6 – 2i – 3 – 5i = 3 – 7i.

Below are the properties of operations with complex numbers.

Addition and subtraction