Contents
In this publication, we will consider the Vieta theorem, which determines the relationship between the coefficients of a polynomial and its roots, and also learn how to apply it in practice to solve problems.
Statement of the theorem
If c1, C2…, cn are the roots of the polynomial xn + a1xn−1 + a2xn−2 +… + An, where each root is taken the number of times corresponding to its multiplicity, then:
odds a1,2…, an can be expressed as symmetric polynomials in roots, i.e.:
- a1 = −(c1 + c2 + … + cn)
- a2 = c1c2 + c1c3 + … + c1cn + c2c3 + … + cn−1cn
- a3 = −(c1c2c3 + c1c2c4 + … + cn−2cn−1cn)
- an−1 = (-1)n−1(c1c2 … cn−1 + c1c2 … cn−2cn + … + c2c3 … cn
- an = (-1)nc1c2 … cn
In other words, (-1)kak equals the sum of all possible products from k roots.
Note: the theorem is named after the French mathematician François Vieta.
Quadratic equation
For the quadratic equation ax2 + bx + c = 0 with roots x1 и x2 rightly:
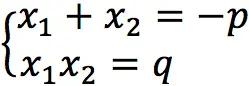
If the equation looks like x2 + px + c = 0 (given form at a = 1), that:
![]()
cubic equation
For the cubic equation p(x) = ax3 + bx2 + cx + d = 0 with roots x1, x2 и x3 rightly:

The converse theorem
If for numbers x1 и x2 relations x1 +x2 = −p, x1x2 =q, so they are the roots of the reduced quadratic equation x2 + px + c = 0.
Examples of tasks
Task 1
Given a quadratic equation x2 − 70x + 600 = 0. Find its roots using Vieta’s theorem.
Decision:
We use the ratio of the roots for the above equation (because a = 1):
x1 +x2 = 70
x1x2 = 600
It remains only to pick up the numbers x1 и x2, which will simultaneously correspond to these equations. In our case, these are 10 and 60.
Task 2
Write an equation if you know that its roots x1 и x2 are 2 and −6, respectively.
Decision:
Suppose we have a reduced quadratic equation of the form x2 + px + c = 0. In this case, based on the root ratios established for it, we obtain:
p = −(x1 +x2) = −(2 + (−6)) = 4
q = x1x2 = 2 ⋅ (−6) = −12
We obtain an equation by substituting the found values into a general formula: x2 + 4x − 12 = 0.









