In this publication, we will consider what types of matrices exist, accompanying them with practical examples to demonstrate the theoretical material presented.
Recall that matrix – This is a kind of rectangular table consisting of columns and rows that are filled with certain elements.
Types of matrices
1. If the matrix consists of one row, it is called row vector (or matrix-row).
Example:
![]()
2. A matrix consisting of one column is called column vector (or matrix-column).
Example:

3. Square is a matrix that contains the same number of rows and columns, i.e. m (strings) equals n (columns). The size of the matrix can be given as n x n or m x mWhere m (n) – her order.
Example:

4. Zero is a matrix, all elements of which are equal to zero (aij = 0).
Example:

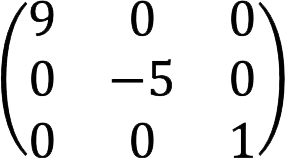
5. Diagonal is a square matrix in which all elements, with the exception of those located on the main diagonal, are equal to zero. It is simultaneously upper and lower triangular.
Example:
6. Single is a kind of diagonal matrix in which all elements of the main diagonal are equal to one. Usually denoted by the letter E.
Example:
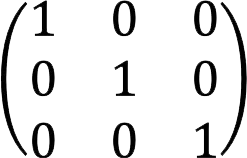
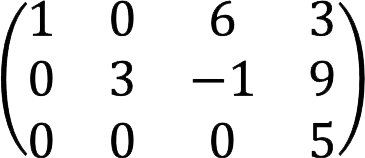
7. Upper triangular – all elements of the matrix below the main diagonal are equal to zero.
Example:

8. lower triangular is a matrix, all elements of which are equal to zero above the main diagonal.
Example:
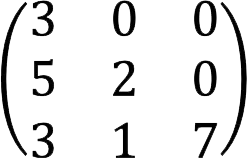
9. stepped is a matrix for which the following conditions are satisfied:
- if there is a null row in the matrix, then all other rows below it are null.
- if the first non-null element of a particular row is in a column with an ordinal number j, and the next row is non-null, then the first non-null element of the next row must be in a column with a number greater than j.
Example: