Contents
In this publication, we will consider various types of straight line equations, accompanying them with practical examples (graphs) for a better understanding of the theoretical material.
Types of straight line equations
Cartesian coordinate system
The general equation of a straight line looks like this:
Ax + By + C = 0
where A, B и C are arbitrary constants.
Wherein:
- A и B cannot simultaneously take on a null value;
- If A = 0, then a straight line parallel to the x-axis (Ox);
- If B = 0, then the line parallel to the y-axis (Moon);
- If C = 0, then the straight line passes through the origin.
Example: this is how the graph of the straight line given by the equation looks like

Slope Equation
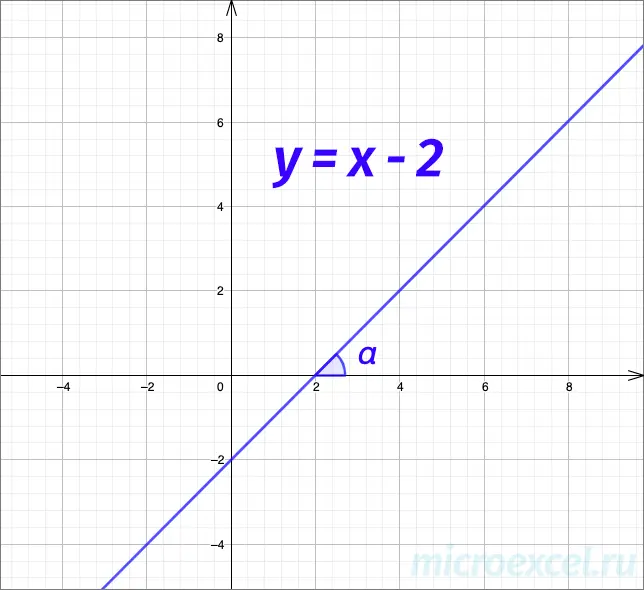
Another common and, perhaps, more familiar way of writing the equation of a straight line:
y = kx + b
- k – angular coefficient, k = tg α;
- α is the angle between the positive directions of the straight line and the x-axis.
Example: graph of the straight line given by the equation
Notes:
- RџSЂRё k = 0 the line will be parallel to the axis Ox.
- straight line parallel to the axis Oy, cannot be expressed in terms of such an equation.
Equation in segments
A line that intersects the x-axis at a point (a, 0) and here is the ordinate at the point (0, b), is written as follows:
![]()
where a ≠ 0, b ≠ 0.
Example:

Note: using such an equation, it will not be possible to write a straight line that passes through the origin.
normal equation
x cos α + y without α – p = 0
- p is the length of the perpendicular drawn to the straight line from the origin;
- α – the angle between the positive directions of the perpendicular and the abscissa axis.
Example:

Note: with p = 0 the line passes through the origin.