In this publication, we will consider one of the main theorems in Euclidean geometry, the theorem on the sum of angles of a triangle, and also learn how to apply it in practice to solve problems.
Statement and formula of the theorem
The sum of the angles of any triangle in the plane is 180°.
α + β + γ = 180°
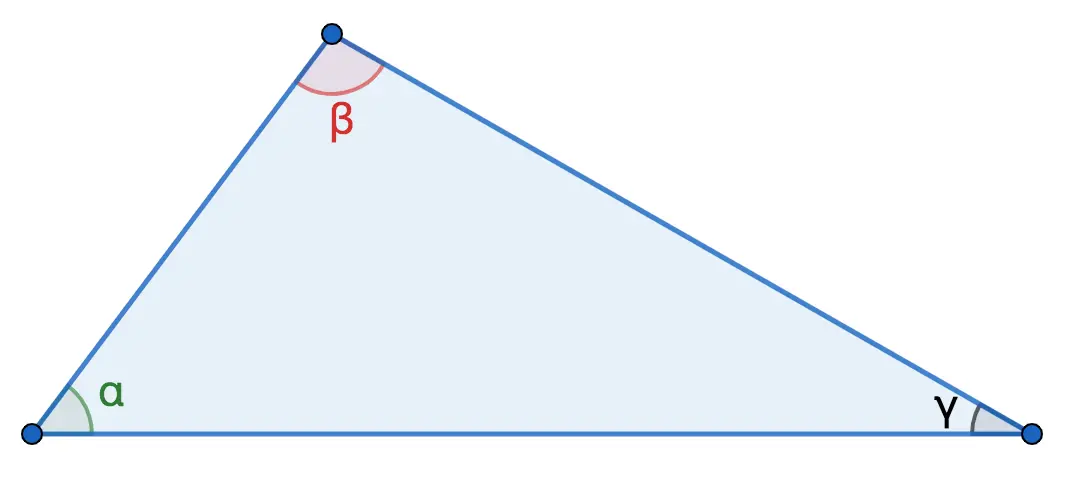
Consequence:
It follows from the theorem that any triangle has two acute angles, i.e. less than 90°.
In our case, this is α и γ.
Examples of tasks
Task 1
Given a triangle whose acute angles are 30° and 43°. Find the value of the third angle.
Decision:
Based on the theorem, the third angle is: 180° – 30° – 43° = 107°.
Task 2
In an isosceles triangle, the angle adjacent to the base is 35°. Find the corner opposite the base.
Decision:
As we know, in an isosceles triangle, the angles at the base are equal, which means that their sum is 70 ° (35 ° * 2). Therefore, the unknown angle is 110° (180° – 70°).









