Three perpendiculars theorem

In this publication, we will consider one of the main theorems in geometry, studied in grades 10-11 – about three perpendiculars. We will also analyze an example of solving the problem to consolidate the material presented.

Statement of the theorem

If a straight line is drawn through the base of an inclined plane perpendicular to its projection, then this straight line will be perpendicular to the inclined itself.

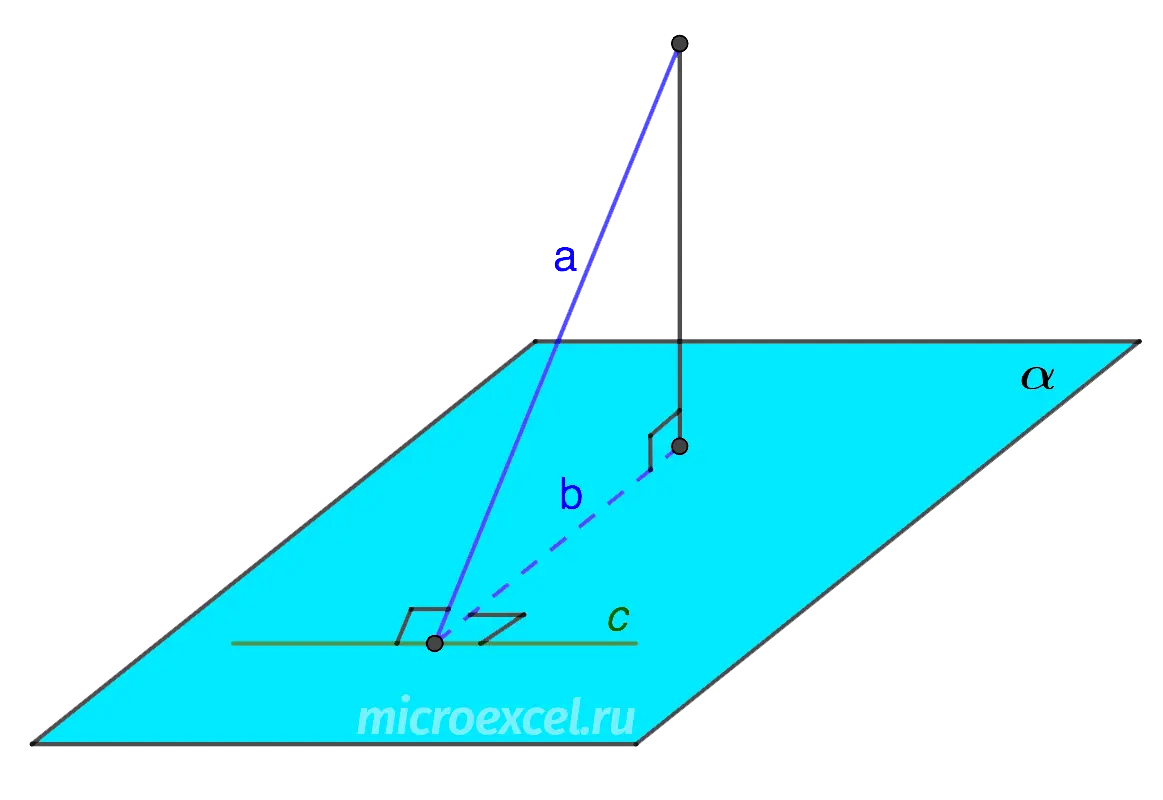
• α – plane;
• a – oblique;
• b is the projection of the oblique (a) on the plane (α);
• c is a straight line on the plane (α) perpendicular to the oblique projection (b).

The converse theorem

If a straight line perpendicular to it is drawn through the base of an inclined plane, then this line will be perpendicular to the projection of the inclined plane on the plane.

Example of a problem

The length of the slope drawn from a point A to the plane α, is equal to 10 cm, and its projection is 6 cm. Find the distance of the point A to the plane.

Solution

Let’s draw the condition of the problem in the form of a drawing below.

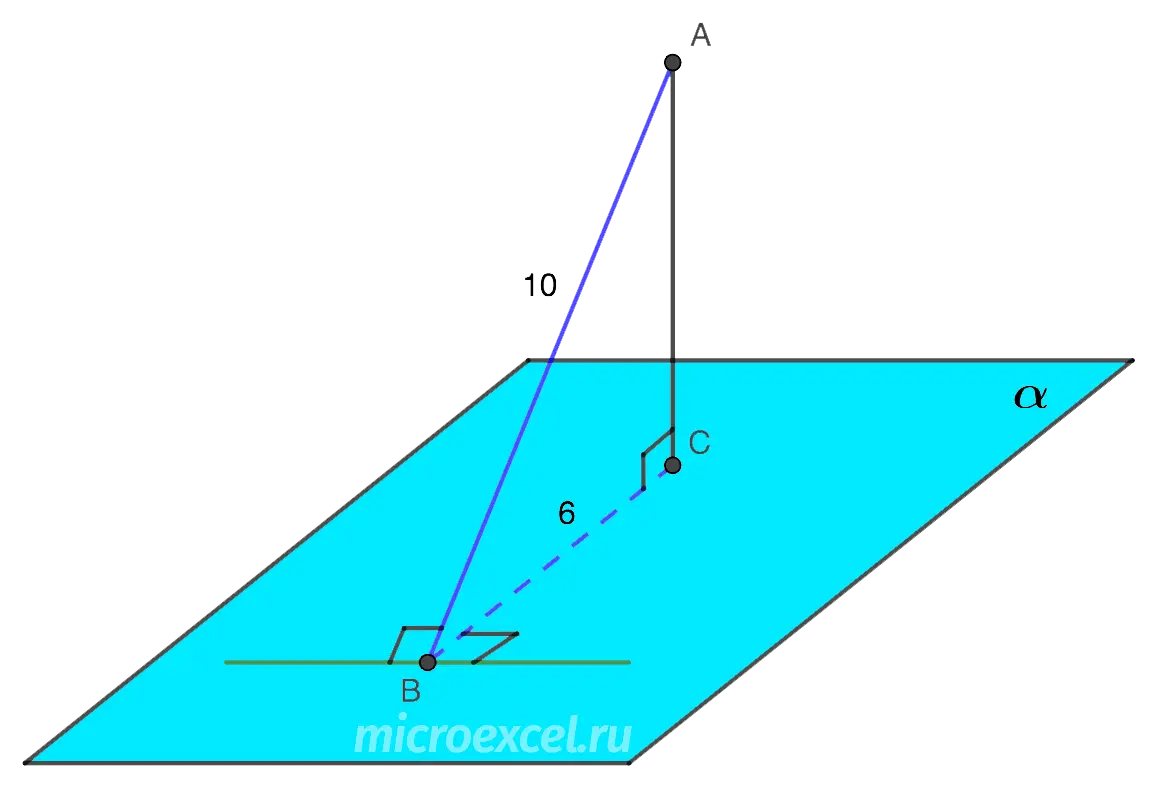
Distance from point A up to the plane α is the length of the segment AC, which is also a leg of a right triangle ABC.

Using the Pythagorean theorem, we get:

AC² =AB² – BC² = 10² – 6² = 64.

Therefore AC = √64 = 8 cm.