The concept of decimal fraction

In this publication, we will consider what a decimal fraction is, how it is written and read, what ordinary fraction it corresponds to and what its main property is. Examples are attached to the theoretical material for better understanding.

Decimal definition

Decimal – this is a special type of recording of an ordinary fraction, the denominator of which is 10, 100, 1000, 10000, etc.

Such fractions, instead of the usual spelling (with a numerator, denominator and a dash-separator), are usually written as follows: 0,3 ; 2,6 ; 5,62 ; 7,238 etc.

Decimals are of two types:

• final – after the decimal point, the final number of digits;
• endless – after the decimal point, the number of digits is infinite. Most often, such fractions are up to 1-3 digits after the decimal point.

Decimal notation

A decimal fraction consists of an integer and a fractional part, between which there is a decimal separator – in the form of a comma or a point.

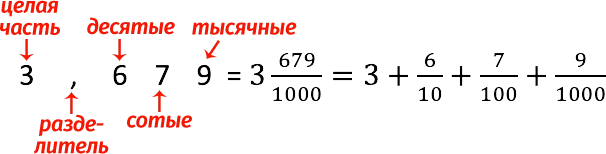
Correspondence to the decimal fraction of an ordinary:

• The integer part (to the left of the comma) is similar to that in the recording (the wrong one should also be converted to mixed). If the fraction is correct (the numerator is less than the denominator), then the integer part is equal to 0.
• The fractional part (to the right of the decimal point) contains the same digits as the numerator of the fractional part if we represented the fraction as an ordinary one.
• The number of digits after the decimal point is limited by what number the numerator in an ordinary fraction is divisible by (the number of digits is equal to the number of zeros after one):
  • 1 digit – out of 10;
  • 2 digits – for 100;
  • 3 digits – per 1000
  • 4 digits – for 10000;
  • etc.

examples:

Note: If in a decimal fraction immediately after the decimal point there are zeros and then only digits, then in the form of an ordinary fraction it looks like this: the numerator is only digits without zeros, the denominator is one and the number of zeros corresponding to the number of digits after the decimal point.

For example:

Reading a decimal

The decimal fraction is read as follows: first, the whole part is pronounced with the addition of the word “whole”, then the fractional part, indicating the digit, which depends on the number of digits after the decimal point:

• 1 digit – “tenths”;
• 2 digits – “hundredths”;
• 3 digits – “thousandths”;
• 4 digits – “ten thousandths”;
• etc.

For example:

• 0,2 – zero point, two tenths;
• 0,54 – zero point, fifty-four hundredths;
• 7,8 – seven whole, eight tenths;
• 12,64 – twelve point sixty-four hundredths;
• 10,056 is ten point fifty-six thousandths.

The main property of a decimal fraction

The value of a decimal fraction will not change if any number of zeros are added to the right of it. Those. if such zeros occur, they can simply be discarded (only those zeros that are located to the right of the numbers in the fractional part).

For example:

• 0,3000 = 0,3;
• 0,25000 = 0,25;
• 2,0500000 = 2,05;
• 16,15400000 = 16,154.