Thales’ theorem: formulation and example of solving the problem

In this publication, we will consider one of the main theorems in class 8 geometry – the Thales theorem, which received such a name in honor of the Greek mathematician and philosopher Thales of Miletus. We will also analyze an example of solving the problem to consolidate the material presented.

Content

Statement of the theorem

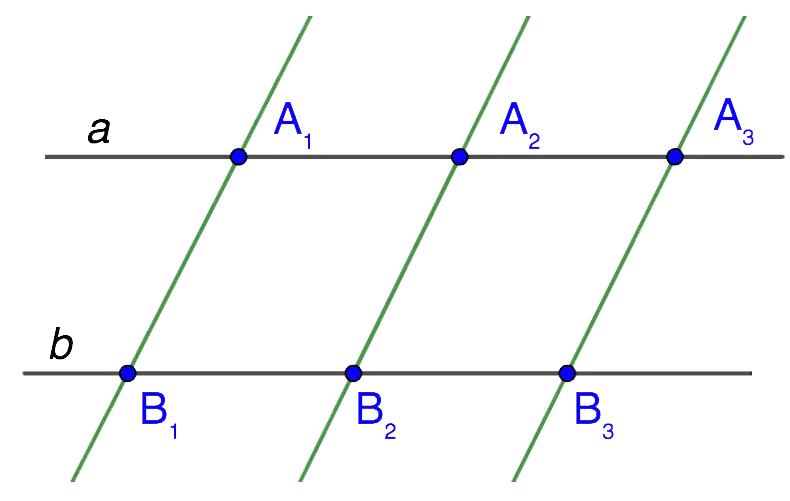
If equal segments are measured on one of the two straight lines and parallel lines are drawn through their ends, then crossing the second straight line they will cut off segments equal to each other on it.

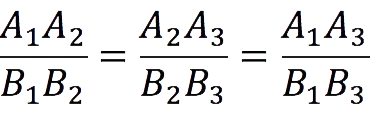
Thales theorem: formulation and example of solving the problem

  • A1A2 = A2A3 …
  • B1B2 =B2B3 …

Note: The mutual intersection of the secants does not play a role, i.e. the theorem is true both for intersecting lines and for parallel ones. The location of the segments on the secants is also not important.

Generalized formulation

Thales’ theorem is a special case proportional segment theorems*: parallel lines cut proportional segments at secants.

In accordance with this, for our drawing above, the following equality is true:

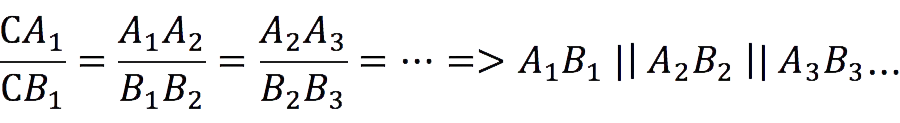
Thales theorem: formulation and example of solving the problem

* because equal segments, including, are proportional with a coefficient of proportionality equal to one.

Inverse Thales theorem

1. For intersecting secants

If lines intersect two other lines (parallel or not) and cut off equal or proportional segments on them, starting from the top, then these lines are parallel.

Thales theorem: formulation and example of solving the problem

From the inverse theorem follows:

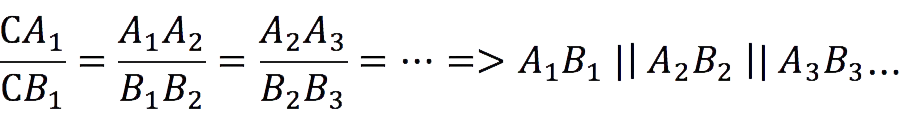
Thales theorem: formulation and example of solving the problem

Required condition: equal segments should start from the top.

2. For parallel secants

The segments on both secants must be equal to each other. Only in this case the theorem is applicable.

Thales theorem: formulation and example of solving the problem

  • a || b
  • A1A2 =B1B2 = A2A3 =B2B3 …

Example of a problem

Given a segment AB on surface. Divide it into 3 equal parts.

Thales theorem: formulation and example of solving the problem

Solution

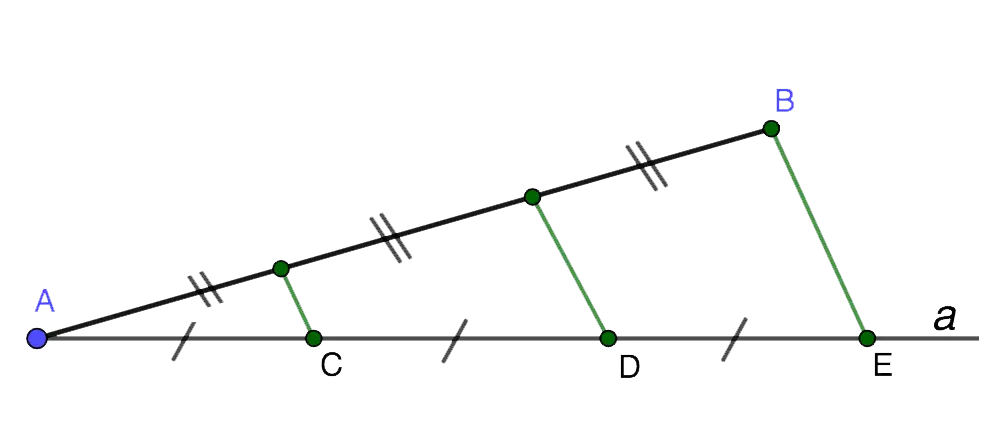
Thales theorem: formulation and example of solving the problem

Draw from a point A direct a and mark on it three consecutive equal segments: AC, CD и DE.

extreme point E on a straight line a connect with dot B on the segment. After that, through the remaining points C и D parallel BE draw two lines that intersect the segment AB.

The points of intersection formed in this way on the segment AB divide it into three equal parts (according to the Thales theorem).

Leave a Reply