In this publication, we will consider one of the abbreviated multiplication formulas, namely, the square of the sum. We will also analyze examples of solving problems to consolidate the material presented.
Sum square formula
The square of the sum of the terms a и b equals a square a plus double product a и b plus square b.
(a+b)2 = A2 + 2ab + b2
The expression can also be presented in reverse order:
a2 + 2ab + b2 = (a + b)2
Proof of the formula
Arithmetic
Let’s represent the formula as a product of two identical brackets (in other words, multiply the expression by itself):
(a+b)(a+b).
Now let’s open the brackets according to the arithmetic rules and get:
(a+b)(a+b) = a2 + ab + ba + b2 = A2 + 2ab + b2.
Geometric
In order to prove the formula geometrically, we draw a square, which is divided into four parts using two segments in such a way that we get:
- two squares with different side lengths (a or b);
- 2 rectangles with the same length (a) and width (b).
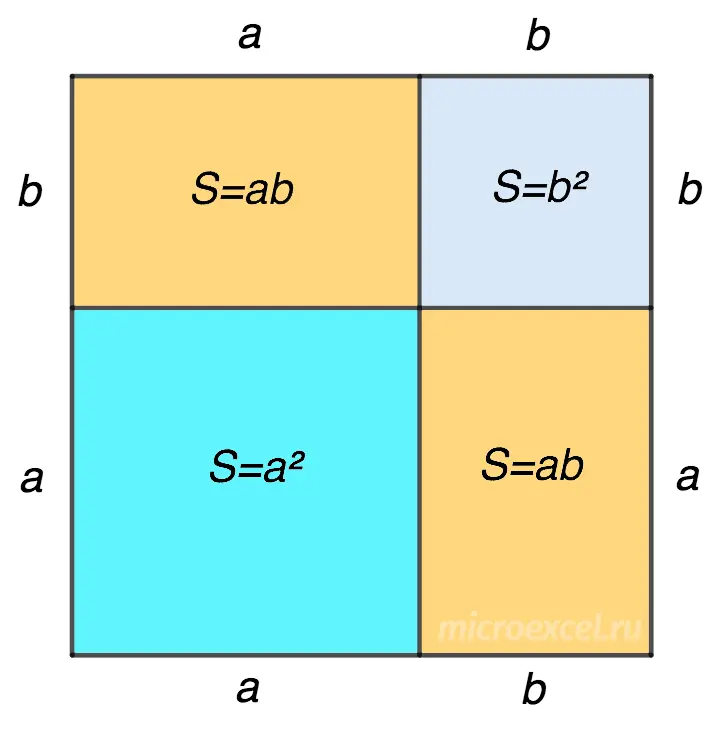
The area of the large square is (a+b)2 and, at the same time, the sum of the areas of the figures that make up:
Ssq. = (a + b)2 = A2 + ab + ab + b2 = A2 + 2ab + b2.
Examples of tasks
The task
What is the square of the sum (2x + 4y3)2?
Solution
Let’s use the abbreviated multiplication formula:
(2x + 4y3)2 = (2x)2 + 2 ⋅ 2x ⋅ 4y3 + (4y3)2 = 4x2 + 16xy3 + 16y6
Note:
The formula can be used for quick mental calculations, for example:
- 632 = (60 + 3)2 = 602 + 2 ⋅ 60 ⋅ 3 + 32 = 3600 + 360 + 9 = 3969.
- 942 = (90 + 4)2 = 902 + 2 ⋅ 90 ⋅ 4 + 42 = 8100 + 720 + 16 = 8836.









