Contents
In this publication, we will consider how to find the sum and difference of vectors, we will give a geometric interpretation, as well as formulas, properties and examples of these actions.
Sum of vectors
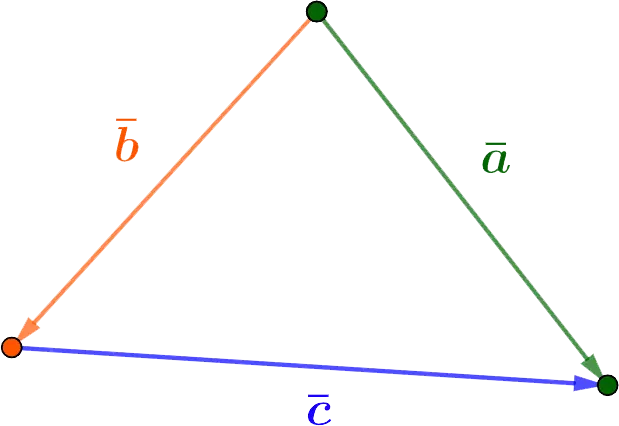
Vector addition is performed according to triangle rule.
Geometric interpretation:
sum a и b is a vector c, whose beginning coincides with the beginning a, and the end – with the end b. In this case, the end of the vector a must match the beginning of the vector b.
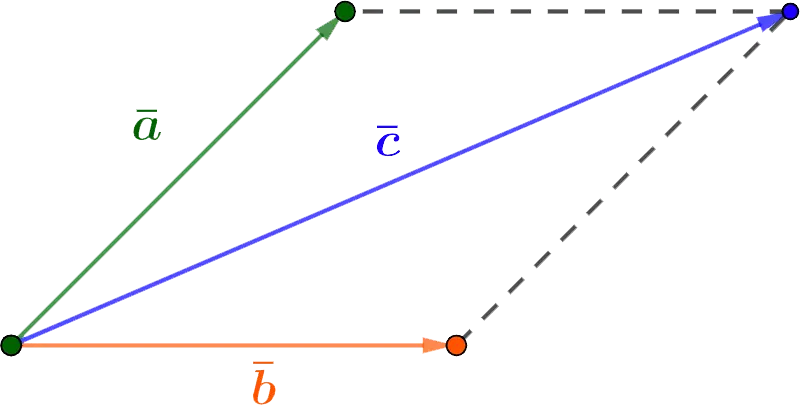
Also used for vector addition parallelogram rule.
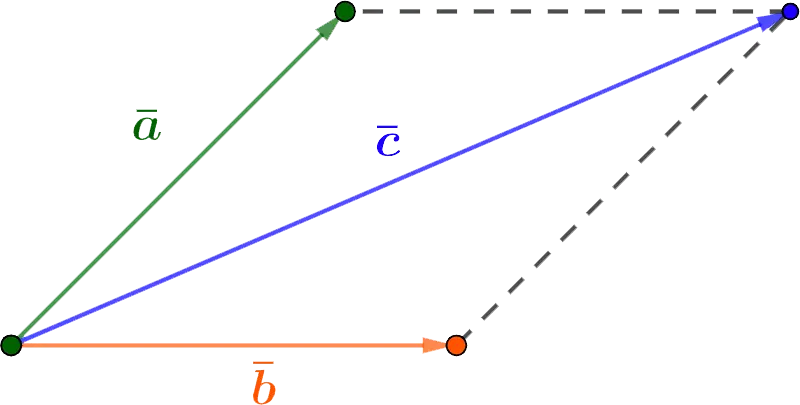
Two non-collinear vectors a и b can be reduced to a common origin, in which case their sum is the vector c, coinciding with the diagonal of the parallelogram and originating at the same point as the original vectors.
Vector addition formula
ci = Ai + bi
Vector elements c are equal to the pairwise sum of the corresponding elements a и b.
| For flat tasks | For XNUMXD tasks | For n-dimensional vectors | Свойства сложения векторов 1. Коммутативность: a + b = b + a 2. Ассоциативность: (a + b) + c = a + (b + c) 3. Прибавление к нулю: a + 0 = a 4. Сумма противоположных векторов: a + (-a) = 0 Примечание: Вектор –a коллинеарен и равен по длине a, но имеет противоположное направление, из-за чего называется противоположным. Разность векторовДля вычитания векторов также применяется правило треугольника.
If from vector a subtract b, then it will work c, and the following condition must be met: Vector subtraction formulaci = Ai – bi Vector elements c are equal to the pairwise difference of the corresponding elements a и b.
|