Stewart’s theorem: formulation and example with solution

In this publication, we will consider one of the main theorems of Euclidean geometry – Stewart’s theorem, which received such a name in honor of the English mathematician M. Stewart, who proved it. We will also analyze in detail an example of solving the problem to consolidate the presented material.

Statement of the theorem

Dan triangle ABC. By his side AC point taken D, which is connected to the top B. We accept the following notation:

• AB = a
• BC = b
• BD = p
• AD = x
• DC = and

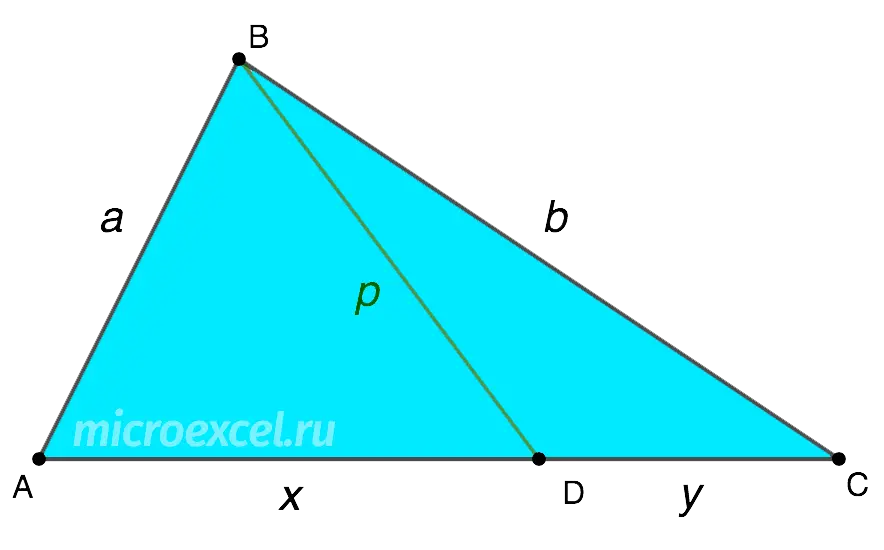
For this triangle, the equality is true:

Application of the theorem

From Stewart’s theorem, formulas can be derived for finding the medians and bisectors of a triangle:

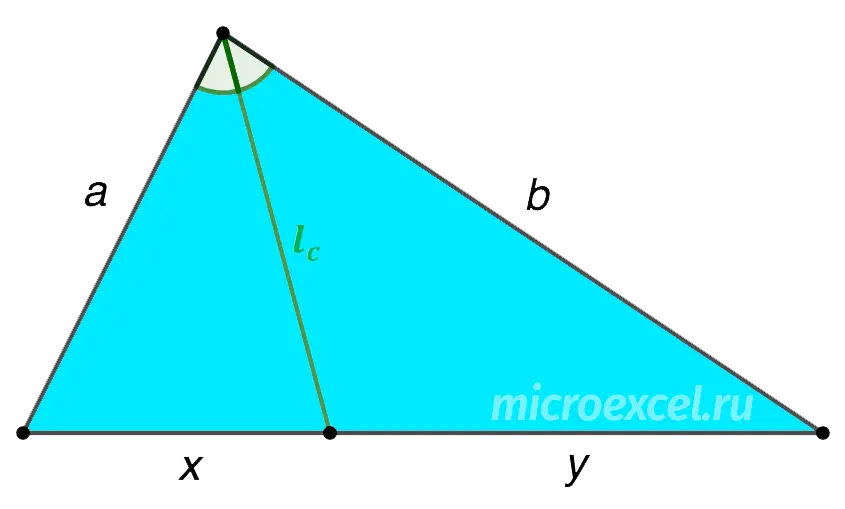
1. The length of the bisector

Let l_c is the bisector drawn to the side c, which is divided into segments x и y. Let’s take the other two sides of the triangle as a и b… In this case:

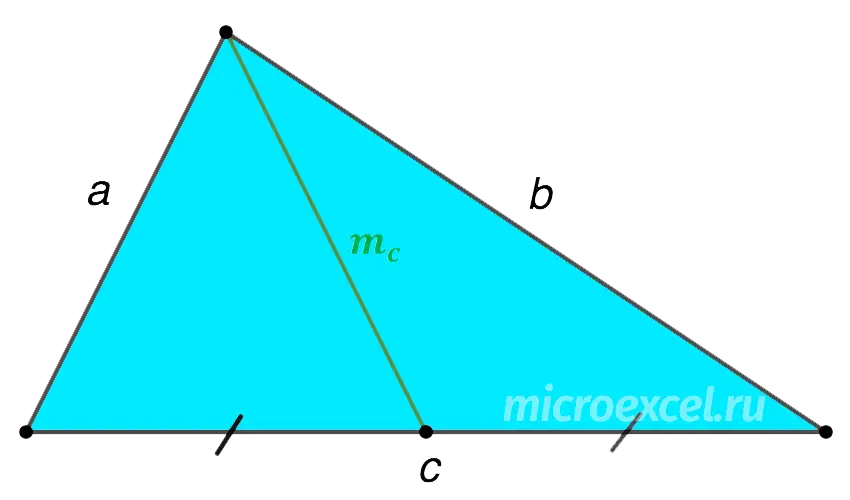
2. Median length

Let m_c is the median turned down to the side c. Let’s denote the other two sides of the triangle as a и b… Then:

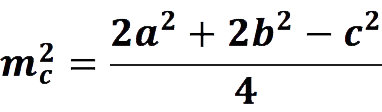
Example of a problem

Triangle given ABC. On the side AC equal to 9 cm, point taken D, which divides the side so that AD twice as long DC. The length of the segment connecting the vertex B and point D, is 5 cm. In this case, the formed triangle ABD is isosceles. Find the remaining sides of the triangle ABC.

Solution

Let’s depict the conditions of the problem in the form of a drawing.

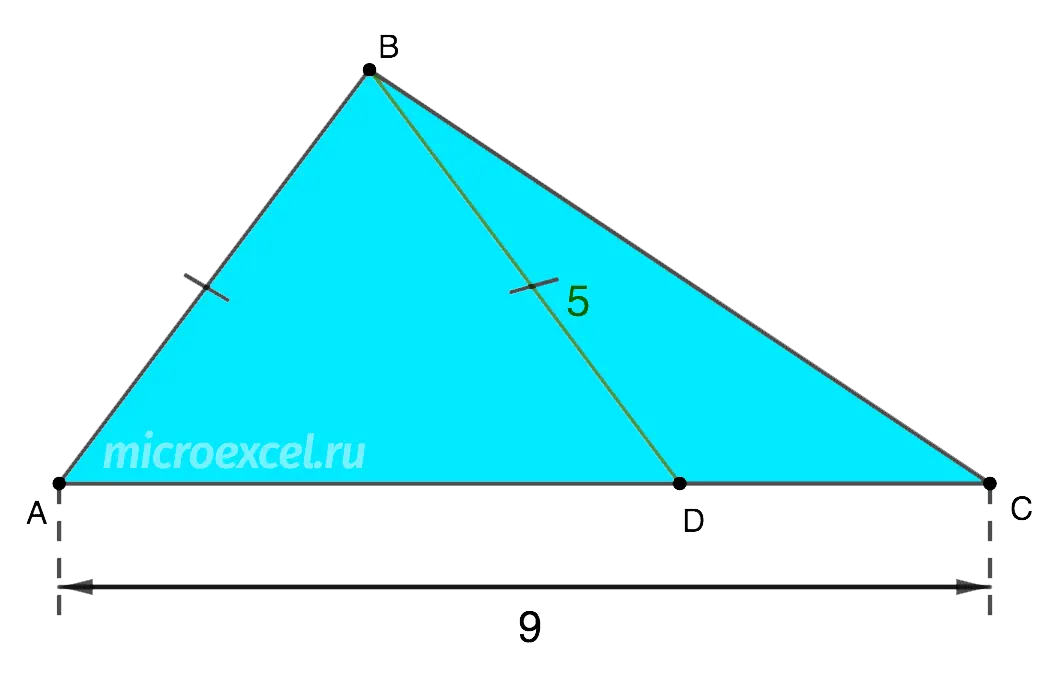
AC = AD + DC = 9 cm. AD longer DC twice, i.e. AD = 2DC.

Consequently, the 2DC + DC = 3DC u9d XNUMX cm. So, DC = 3 cm, AD = 6 cm.

Because triangle ABD – isosceles, and side AD is 6 cm, so they are equal AB и BDIe AB = 5 cm.

It remains only to find BC, deriving the formula from Stewart’s theorem:

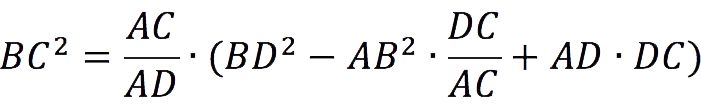
We substitute the known values ​​into this expression:

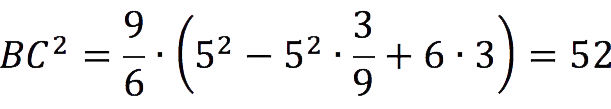
In this way, BC = √‎52 ≈ 7,21 cm.