In this publication, we will look at what the standard form of a number is and how it is written. We will also analyze practical examples on this topic.
Writing large and small numbers
In the exact sciences, from time to time, very large or, conversely, small values uXNUMXbuXNUMXbof quantities are encountered. To make it more comfortable to work with them, and even more so, to use them together in the same calculations, a certain general principle for writing numbers was invented, the so-called standard view.
To fully assimilate the material presented below, you need to know what a degree is. For example, let’s demonstrate its different variants on the number 10:
- 10-3 = 0,001
- 10-2 = 0,01
- 10-1 = 0,1
- 100 = 1
- 101 = 10
- 102 = 100
- 103 = 1000
Also recall that in order to multiply a number by 10, 100, 1000, 10000, etc., we simply attribute to it the number of zeros that is contained in 10, 100, 1000, 10000, etc. For example,
- 3 10 = 30
- 43 100 = 4300
- 17 1000 = 17000
The same goes for dividing by 10, 100, 1000, 10000, etc., only here we remove zeros:
- 650: 10 = 65
- 1400: 100 = 14
- 78000: 1000 = 78
The actions listed above can be represented in another form – as a product of 10 to a certain extent:
- positive if multiplication by 10, 100, 100, etc. is performed;
- negative if division is being performed.
For example:
- 3 · 10 = 3 · 101 = 30
- 17 · 1000 = 17 · 103 = 17000
- 1400 : 100 = 1400 · 10-2 = 14
Decimal fractions
If we are dealing with decimal fractions, then in general everything is the same. When they are multiplied by 10, 100, 1000, etc. we shift the separator comma to the right as many positions as there are zeros in 10, 100, 1000, and so on.
- 6,2 10 = 6,2 101 = 62
- 2,31 · 100 = 2,31 · 102 = 231
- 0,147 · 1000 = 0,147 · 103 = 147
- 3,106 · 10000 = 3,106 · 104 = 31060
If we need to divide a decimal by 10, 100, 1000, etc., then we shift the comma to the left by the number of positions corresponding to zeros:
- 34 : 10 = 34 · 10-1 = 3,4
- 19 : 100 = 19 · 10-2 = 0,19
- 27 : 1000 = 27 · 10-3 = 0,027
Standard form of number
A natural number or a decimal fraction (final) can be generally represented as follows:
a · 10n, where:
- a и n – integers;
- 0 ;
- n – order of number a.
Such a record is standard form of a number.
Example 1
Let’s represent the number 2300 in standard form.
Decision:
The first digit of the number is 2, it is between zero and ten, which satisfies the condition above.
We put a comma-separator after the deuce and count how many digits we have left after it on the right. In our case, there are three.

Therefore, we multiply the resulting decimal fraction (a) by the number 10, the power of which is equal to the number of digits after the decimal point:
2,300 · 103 =
In other words, we have multiplied the fraction by 1000 (103).
As we know, zeros at the end of the decimal part can be omitted in decimal fractions, i.e. the final entry of the number 2300 in standard form looks like this:
2300 = 2,3 103
Example 2
Let’s represent the number 0,0029 in standard form.
Decision:
We need a number from 1 to 9 before the comma (i.e. to the left of it). Therefore, we move the comma three positions to the right.
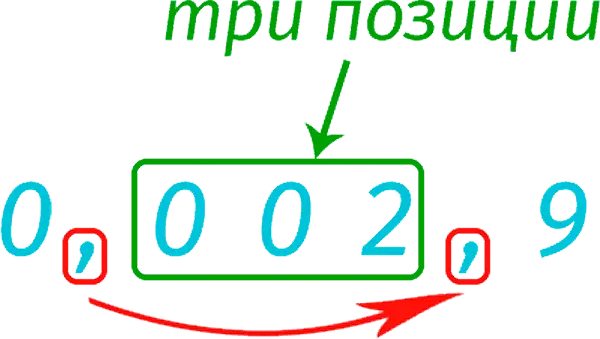
We get a new decimal fraction 2,9. It must be multiplied by 10, but in a negative degree, because. we made the number a multiple of the original. The degree value is equal to the number of positions by which the comma was shifted, i.e. in our case it turns out “minus three”.
2,9 · 10-3 =
In other words, we divide the number 2,9 by 1000 or multiply by 0,001 (10-3).









