In this publication, we will consider what a square root is, give examples, list the main properties, and also demonstrate what the graph of its function looks like.
Definition of the square root
Arithmetic square root of a number a – this is the number x, which when squared (or in other words to the second power) gives the number a.
That is
The square root (sometimes also called the root of the second degree) is indicated by a special sign – √. for example √4, reads like “square root of four”.
Another type of recording
. But the number 2 is usually omitted, meaning exactly it.
Radical expression for the example above, it is 4. However, it can be represented not only by a number, but also by a mathematical expression containing both letters and numbers. For example,
Value Calculation x called taking the square root from the number a (is the inverse of squaring):
- √4 = 2
- √9 = 3
- √16 = 4
- √25 = 5
You can only take the square root of a positive number. In this case, the answer (x) will also always be greater than zero.
Note:
- √0 = 0
- √1 = 1
For convenience, you can learn or always have at hand, at least up to 10-20.
Square root properties
- Product root:
√a ⋅ b = √a ⋅ √b - Division root:
√a : b = √a : √b - Root as exponentiation:
√a = a 1/2 - Adding or subtracting roots is not equal to the root of the sum or difference:
√a ± b ≠ √a ± √b .
Also applicable to the square root.
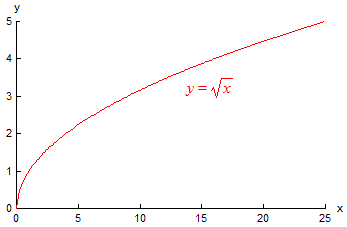
square root plot
On the coordinate plane, the function
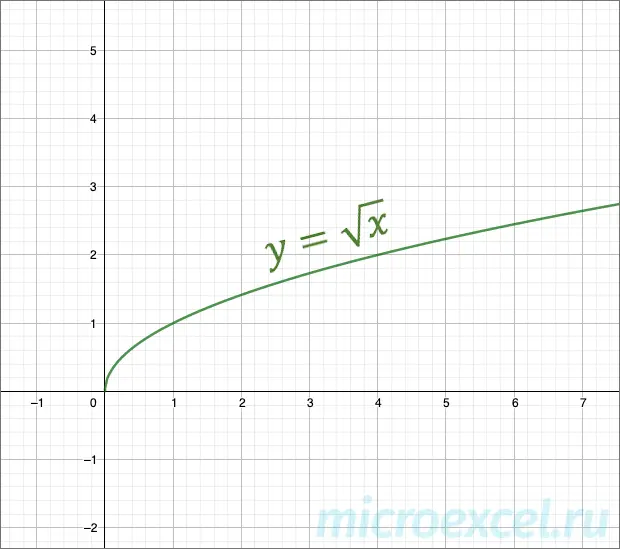
The graph starts at the point