In this publication, we will consider what a system of linear inequalities is, how it is solved by the method of intervals on the real axis. We will also analyze practical examples on this topic.
Definition of a system of inequalities
To solve a system of inequalities, you need to have the skills to deal with linear inequalities. We have discussed this issue in detail in a separate article.
A system of inequalities are two or more inequalities joined by a curly brace. For example:
![]()
Those. she is somewhat similar to, in which “equals” replaced by one of the comparison signs (“greater than”, “less than”, “greater than or equal to”, “less than or equal to”).
Note: in a system of linear inequalities, they are all linear, respectively. Usually there is only one unknown variable in them (most often denoted as “X”).
Solving a system of linear inequalities
The algorithm consists of two main steps:
- We solve each inequality separately.
- We compare the obtained solutions on the numerical axis by the method of intervals, after which we derive the general answer.
Example 1
Let’s try to solve the system above.
Decision:
Now let’s mark the obtained results on the numerical axis, dividing the solution areas with different colors for ease of perception.

We need a site where both solutions are present. As we can see in the figure, it starts with the number 10 inclusive.
Thus, by solving the given system of inequalities:
Example 2
Find the solution to the system of inequalities below:
![]()
Decision:
2x – 5
2x
2x
x
3 (x – 1) + 2 ≥ -13
3x – 3 + 2 ≥ -13
3x ≥ -13 + 3 – 2
3x ≥ -12
x ≥ -4
We transfer the found solutions to the numerical axis and draw the intervals corresponding to them:
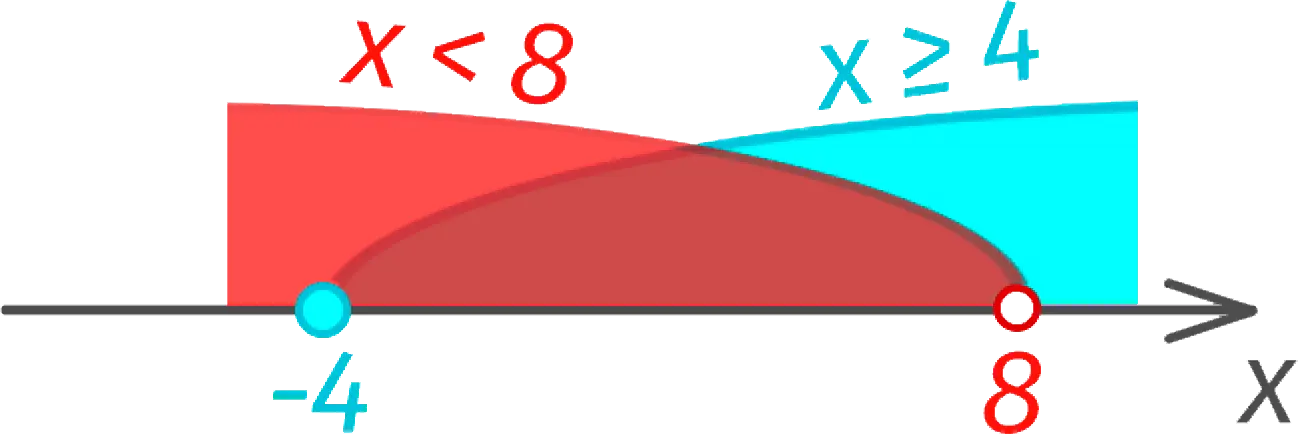
As we can see, the common solution area that satisfies both inequalities is between -4 inclusive and 8 exclusively.
Answer: -4 ≤ x .









