Solving quadratic inequalities

In this publication, we will consider what a quadratic inequality is, and how it is solved by the interval method, depending on the number of roots. We will also analyze practical examples on this topic.

Definition of quadratic inequality

If the highest power of an unknown variable (most often it is x) equals two, then the inequality is called square.

For example:

• x² – 3x + 4 > 0
• 2x² + 7x – 5 < 0
• x² + 12x + 2 ≥ 0
• 3x² – 4 ≤ 0

Solving quadratic inequalities

with two roots

Quadratic equations are solved using the so-called interval method, the principle of which is as follows:

1. We collect all the elements of the inequality on the left side, only zero should remain on the right side. Remember that when an element is transferred from one part to another, its sign changes to the opposite.

2. If there is a negative coefficient in front of the unknown variable in the second degree, we multiply all the elements of the inequality by the number -1, changing the comparison sign to the opposite.

3. Replacing the comparison sign with “equals” solve the resulting quadratic equation.

4. We mark the found roots on the numerical axis.

Moreover, if the comparison sign is strict (“more” or “less”), then the mark is usually an unfilled circle inside, if not strict (“more or equal”, “less or equal”) is shaded.

5. We draw intervals, and from right to left we assign signs to them “a plus” и “minus” (starting with “+”, then alternate).

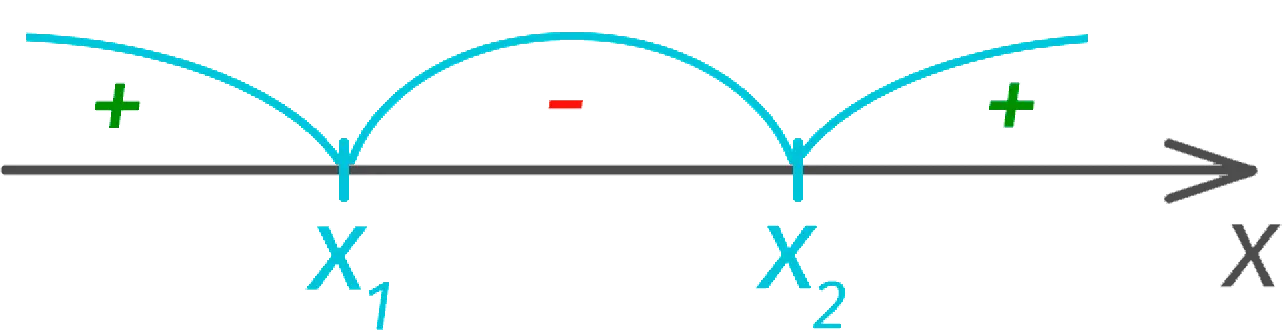
6. If there are signs in the inequality “>“ or “≥“, we need positive intervals if “<“ or “≤“ – negative.

Example 1

Let’s solve the quadratic inequality x² + 4x > -3.

Decision:

1. Because the right side must be zero, we move the number -3 to the left, replacing its sign with “a plus”:

x² + 4x + 3 > 0

2. Now let’s find the roots of the quadratic equation x² + 4x + 3 = 0.

We considered this issue in detail in a separate one, so we will not dwell on this separately here.

So, the roots of the given equation: x₁ =-1, x₂ =-3. We mark them on the numerical axis (open circles, because the inequality is strict).

We draw intervals, marking with signs “a plus” и “minus”.

We need only positive areas, because there is a sign in the inequality “more”.

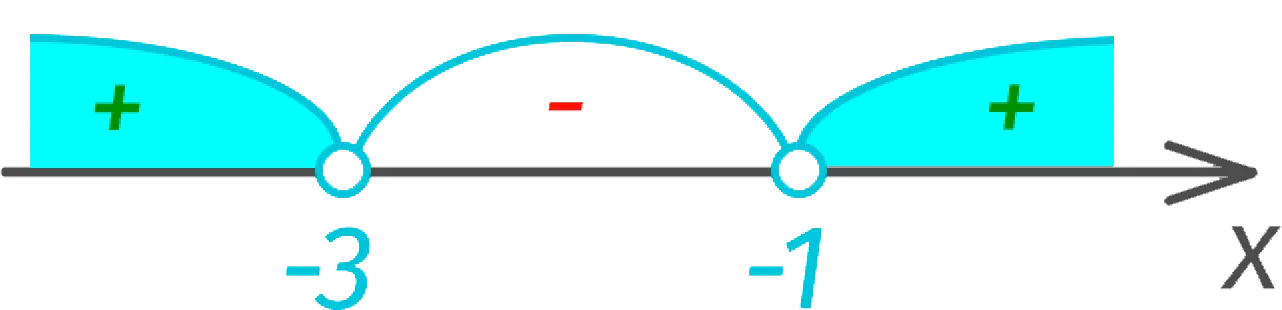
Thus, the solution to the inequality is the following:

x > -1 и x < -3.

Note: if there were other signs in the inequality we are considering, the solution area would be as follows:

• sign “<", then -3 < x < -1
• sign “≥”, then x ≥ -1 и x ≤ -3
• sign “≤”, then -3 ≤ x ≤ -1

with one root

Quadratic equations do not always have two roots, sometimes it can be one.

Example 2

Let’s decide x² – 4x + 4 < 0.

Decision:

The corresponding quadratic equation has only one root: x₁ = x₂ = 2, i.e. its meaning is repeated twice.

We mark a point in the form of an empty circle on the numerical axis and draw two intervals emanating from it.

Now you need to assign signs to the intervals, and here this procedure differs from the one described above (when the equation has two roots): if the value of the root in the equation is repeated an even number of times, then the sign does not change when the intervals change. We put them down, also, from right to left, starting with “plus”.

In our case, the value is repeated twice, i.e. we get:

We only need negative intervals, and they are not here. Moreover, the inequality is strict. Therefore, he has no solutions.

Note: if this inequality had other signs, the solution area would be as follows:

• sign “>”, then x > 2 и x <2
• sign “≥”, then x ≥ 2 и x ≤ 2, i.e. all real numbers.
• sign “≤”, the only solution is x = 2

without roots

In some cases, quadratic equations may not have real roots at all.

In this case, the corresponding inequality will also have no real solutions. This will be the answer.

Example 3

x² + 3x + 5 > 0

Decision:

The equation has no roots, therefore, the inequality has no real solutions.