Solving quadratic equations

Quadratic equation is a mathematical equation, which in general looks like this:

ax² + bx + c = 0

This is a second order polynomial with 3 coefficients:

• a – senior (first) coefficient, should not be equal to 0;
• b – average (second) coefficient;
• c is a free element.

The solution to a quadratic equation is to find two numbers (its roots) – x₁ and x₂.

Formula for calculating roots

To find the roots of a quadratic equation, the formula is used:

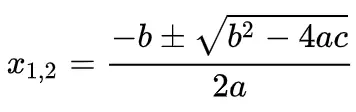
The expression inside the square root is called discriminant and is marked with the letter D (or Δ):

D = b² – 4ac

In this way, The formula for calculating the roots can be represented in different ways:

1. If D > 0, the equation has 2 roots:

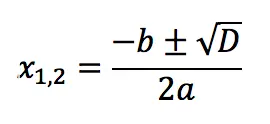
2. If D = 0, the equation has only one root:

3. If D < 0, вещественных корней нет, но есть комплексные:

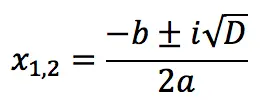
Solutions of quadratic equations

Example 1

3x² + 5x + 2 = 0

Decision:

a = 3, b = 5, c = 2

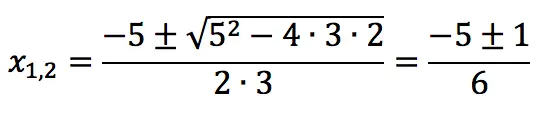
x₁ = (-5 + 1) / 6 = -4/6 = -2/3

x₂ = (-5 – 1) / 6 = -6/6 = -1

Example 2

3x² – 6x + 3 = 0

Decision:

a = 3, b = -6, c = 3

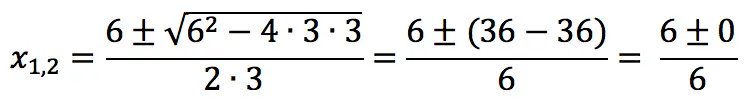
x₁ = x₂ = 1

Example 3

x² + 2x + 5 = 0

Decision:

a = 1, b = 2, c = 5

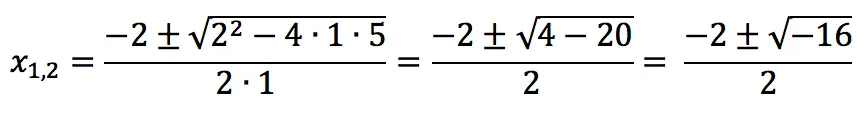
In this case, there are no real roots, and the solution is complex numbers:

x₁ = -1 + 2i

x₂ = -1 – 2i

Graph of a quadratic function

The graph of the quadratic function is a parable.

f(x) = ax² + bx + c

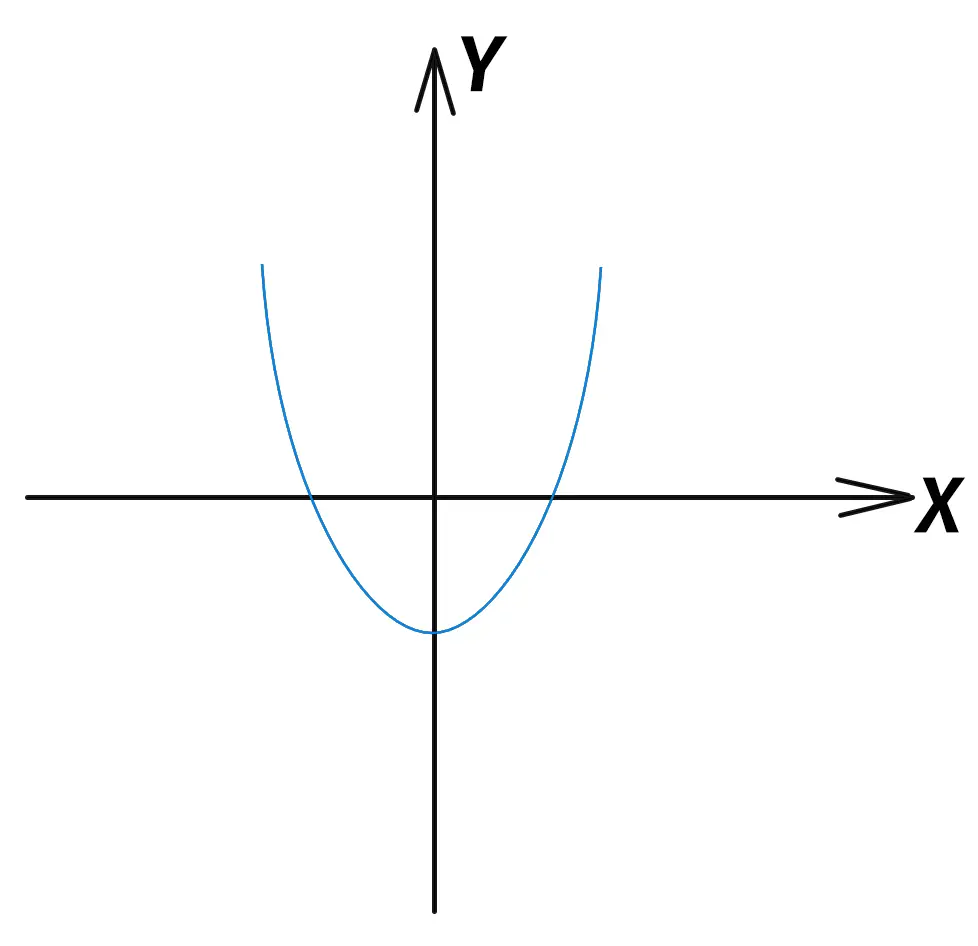
• The roots of a quadratic equation are the points of intersection of the parabola with the abscissa axis (X).
• If there is only one root, the parabola touches the axis at one point without crossing it.
• In the absence of real roots (the presence of complex ones), a graph with an axis X does not touch.