In this publication, we will consider what equations with a modulus (including with two) are, and also demonstrate how they can be solved using practical examples.
Note: what is the modulus of a number, we examined in a separate.
Appearance of equations
Modulo equations might look something like this:
- | x | = 6
(modulo x equals 6)
- |x – 11| = 3
(modulo x minus 11 equals 3)
- |x + 4| = 9
(modulo x plus 4 equals 9)
Those. an unknown variable is specified in the module (just x or an expression including x).
Solving Equations
Let’s break down the solution to each of the above examples.
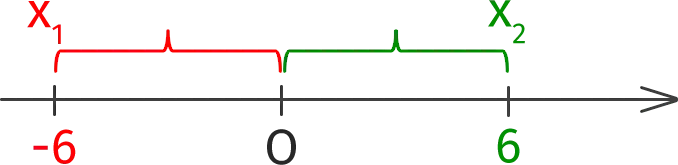
| x | = 6
This means that there are two points on the number line, the distance from which to zero is six. Those. these are points -6 and 6, therefore, this equation has two roots:
|x – 11| = 3
In this case, on the real axis, the distance from the point x up to point 11 is 3. Thus, the equation has two roots:

|x + 4| = 9
This equation can be rewritten as follows: |x – (-4)| = 9.
Now we can interpret it like this: on the coordinate axis, the point x is at a distance of 9 from point -4. Means,
Note:
Sometimes there may be equations with two modules, for example: |x| = |y|.
In this case, there are also two roots:









