In this publication, we will consider one of the main theorems of Euclidean geometry, the sine theorem, which determines the ratio of sides in a triangle, and also learn how to apply it in practice to solve problems.
Statement and formula of the theorem
1. Ordinary theorem
The sides of a triangle are proportional to the sines of the opposite angles.
![]()
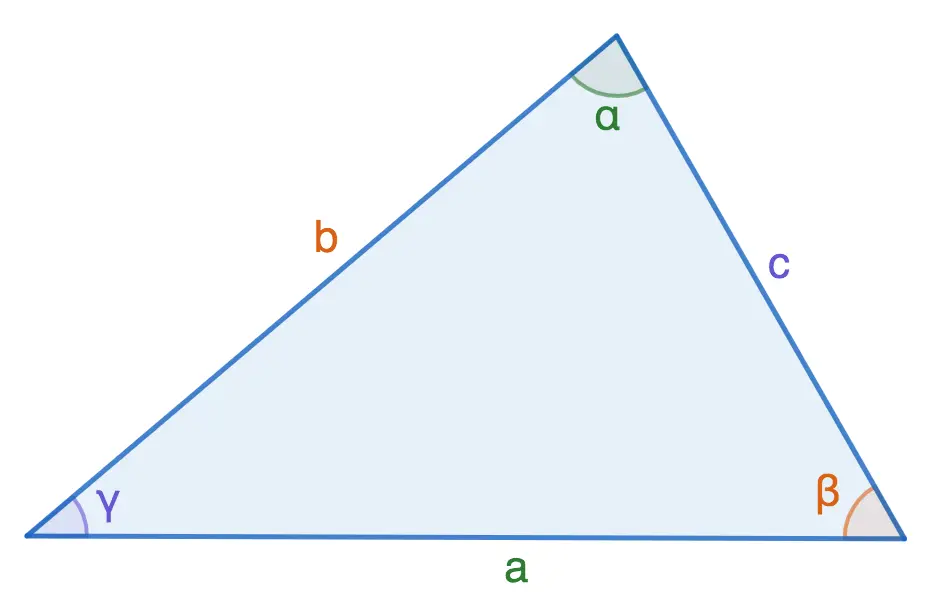
2. Extended theorem
In an arbitrary triangle, the following relation holds:
![]()

R is the radius of the circumscribed circle around the triangle.
Examples of tasks
Task 1
In a triangle, the length of the base is known – 10 cm, the angle opposite the base – 90 °, and also, one of the angles adjacent to it – 45 °. Find the side opposite the 45° angle.
Decision:
Let’s take the unknown side for x and apply the sine theorem:
![]()
Consequently:
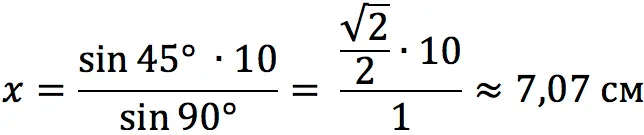
Task 2
The hypotenuse and one of the legs of a right triangle are 10 cm and 8 cm, respectively. Find the angle opposite this leg.
Decision:
As we know, in a right triangle opposite the hypotenuse there is an angle equal to 90 °. Let’s take the unknown angle as x. With that in mind, the aspect ratio looks like this:
![]()
Consequently:
![]()
Hence x = arcsin (4/5) ≈ 53,1°.










