Contents
In this publication, we will consider the definition / designation of similar triangles and three signs of the similarity of figures. We will also analyze an example of solving the problem to consolidate the presented material.
Definition and notation of similar triangles
Similar triangles are called, in which the angles are respectively equal, and the sides of one triangle are proportional to the similar sides of the other.
Related parties in similar triangles, these are the sides opposite their equal angles.
To indicate the similarity of figures, a special symbol “~“. For example, △ABC ∼ △KLM.
Signs of Similar Triangles
Two triangles are similar if one of the following conditions is met.
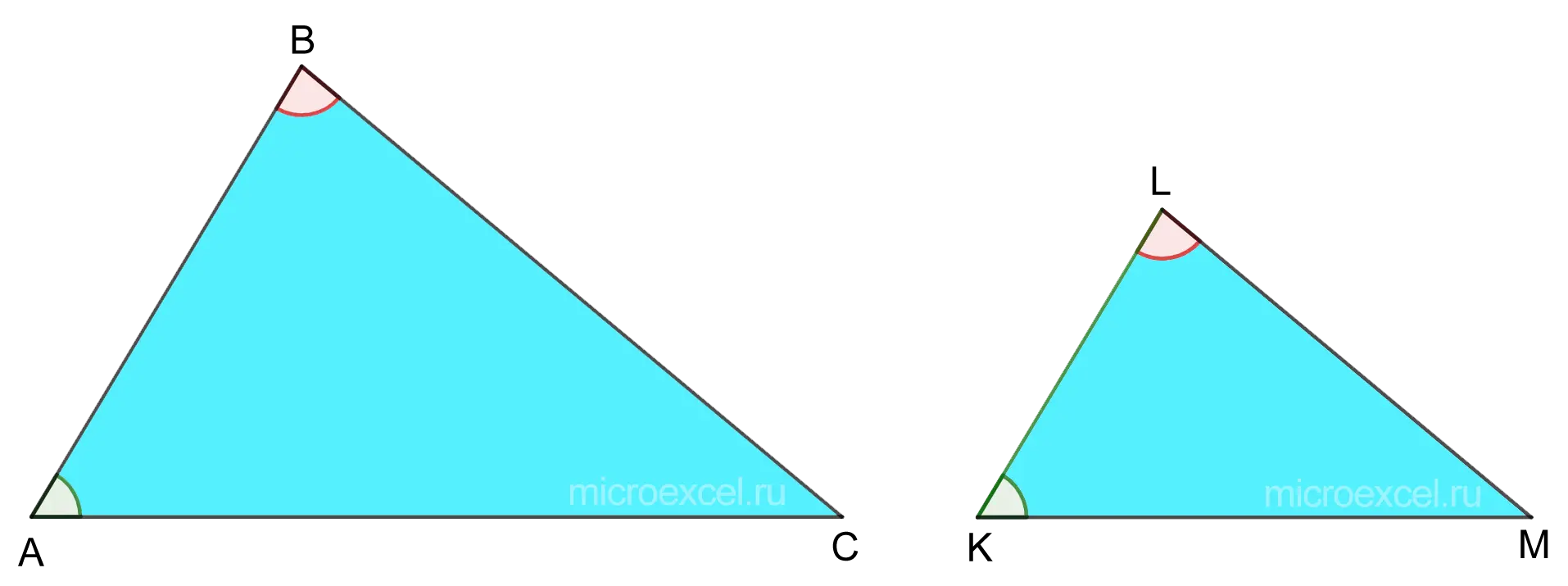
1 sign
Two angles of one triangle are respectively equal to two angles of another.
∠BAC = ∠LKM
∠ABC = ∠KLM
2 sign
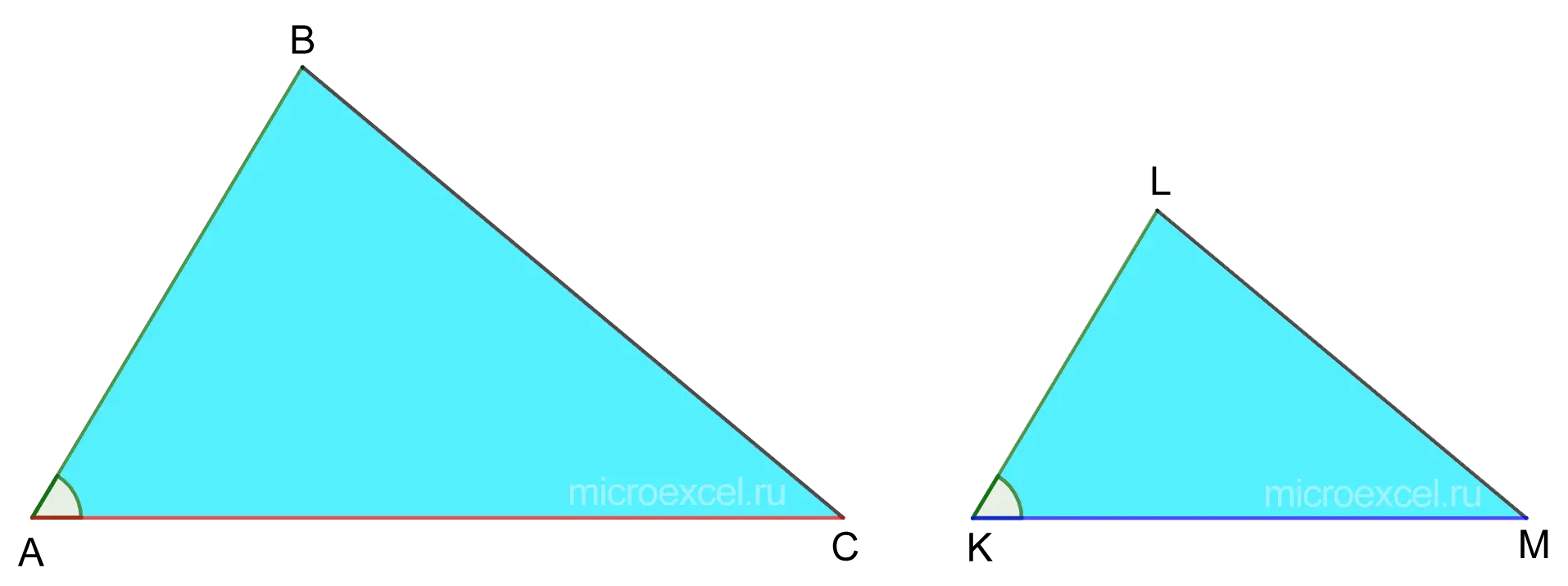
The two sides of one triangle are proportional to the two sides of the other, and the angles between those sides are equal.
∠BAC = ∠LKM
![]()
3 sign
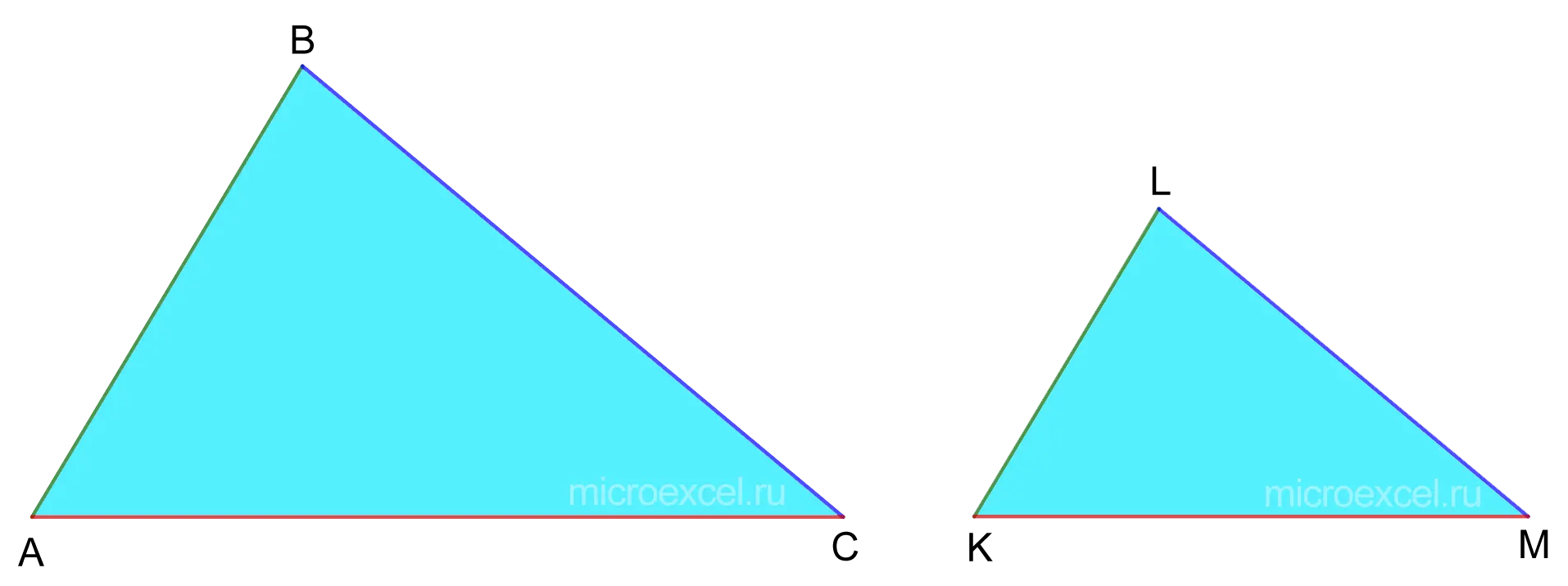
All sides of one triangle are respectively proportional to all sides of the other.
![]()
Example of a problem
Two triangles are given: △ABC with sides 3, 4 and 5 cm; △DEF with sides 6, 8 and 10 cm. Prove that these figures are similar.
Solution
Because Since we know the lengths of all sides, we can check the similarity using the third feature discussed above:
![]()
This equality is true, so it can be argued that △ABC ∼ △DEF.









