In this publication, we will consider the signs of equality of triangles, and also analyze an example of solving the problem in different ways to consolidate the material presented.
Signs of equality of triangles
Two triangles are congruent if one of the conditions below is met.
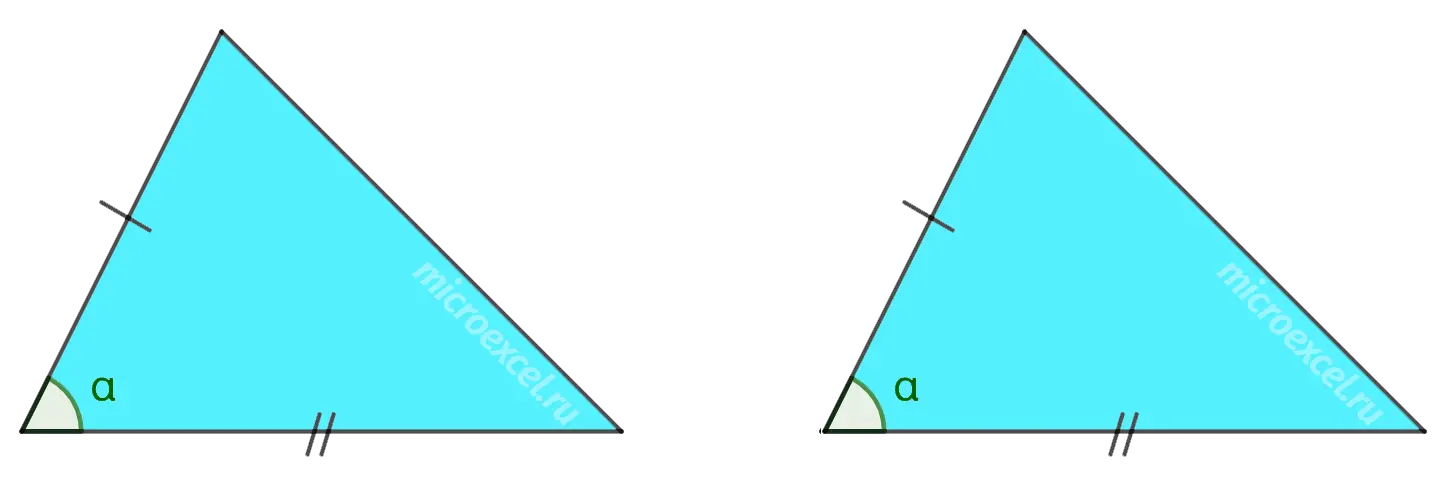
1 sign
The two sides and the angle between them of the first triangle are respectively equal to the two sides and the angle between them of the second triangle.
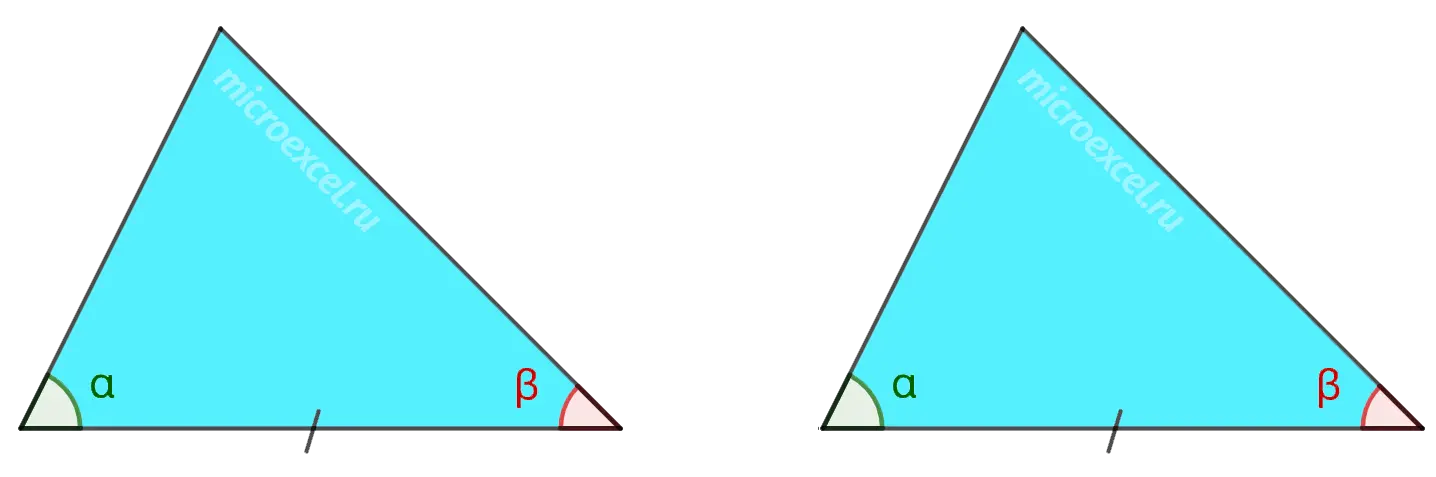
2 sign
The side and two angles adjacent to it of the first triangle are respectively equal to the side and two angles adjacent to it of the second triangle.
3 sign
The three sides of the first triangle are respectively equal to the three sides of the second triangle.
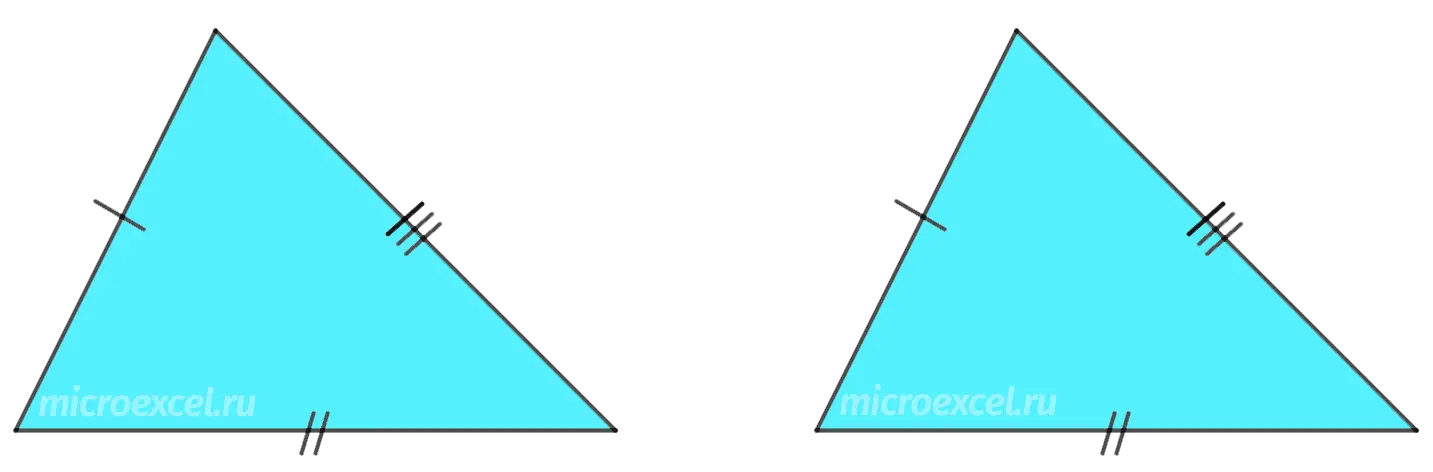
Note: the equality of right-angled triangles, along with the above, is also proved by other criteria.
Example of a problem
Diagonals AC и BD parallelogram ABCD intersect at a point E. Prove that △AED = △BEC.
Solution 1
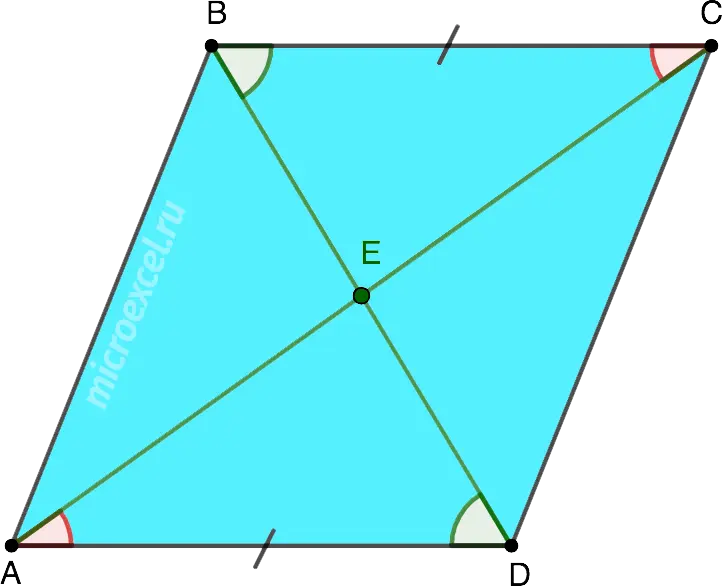
Because it is a parallelogram, its opposite sides are equal, i.e. AD=BC.
Diagonal AC, is also a secant that intersects two parallel lines on which the sides lie AD и BC. As is known, interior cross-lying angles are pairwise equal, therefore, ∠CAD = ∠ACB. Similarly, the angles ∠BDA and ∠DBC.
Hence, the triangles we are considering △AED and △BEC are equal according to the second sign of equality (along the side and 2 angles adjacent to it).
Note: In the same way, one can prove that △General Conditions of Purchase = △CED.
Solution 2

The diagonals of the parallelogram at the point of intersection are divided in half, i.e. AE = EC и BE=ED. Also, the opposite sides of the parallelogram are equal, i.e. BC=AD.
So △AED and △BEC are equal according to the third sign of equality (on three sides).
Note: Similarly, we can prove the equality △General Conditions of Purchase and △CED.
Solution 3

Analyzing solutions 1 and 2, we have already found out that the cross-lying angles are equal, and the diagonals of the parallelogram at the intersection point are divided into two identical parts.
With this in mind, prove the equality of triangles △AED and △BEC (or △General Conditions of Purchase and △CED) is possible by referring to the first feature (on two sides and the angle between them).









