Contents
In this publication, we will consider how decimal fractions can be rounded to different digits of fractional (tenths, hundredths, thousandths, etc.) and integer (units, tens, hundreds, etc.) parts. We will also analyze examples for a better understanding and consolidation of the material.
Decimal rounding rules
Decimals can be rounded up:
- up to an integer with an accuracy of units, tens, hundreds, etc.;
- up to a certain fractional digit: tenths, hundredths, thousandths, ten thousandths, etc.
But, before moving on to the rounding rules, let’s remember once again what a decimal fraction consists of. As an example, from thousands to ten thousandths:
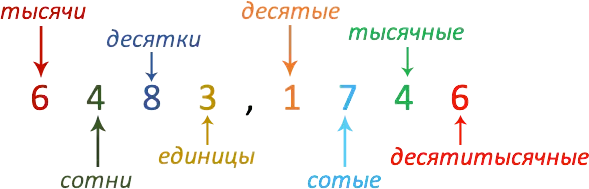
Fractional Rounding
So, in order to round a decimal fraction, we adhere to the following plan of action:
- We mark the digit to which the fraction should be rounded. It can be separated from the following numbers by a dividing line.
- Further, two options are possible (according to the rules for rounding numbers):
- if the selected digit is followed by numbers 0, 1, 2, 3 or 4, then we leave the digit of this digit the same, and remove all other digits after the line.
- if there are numbers after the selected digit 5, 6, 7, 8 or 9, then we add one to the digit of this category and, as in the paragraph above, we remove all the numbers on the right side of the line.
Example 1: round 12,624 up to tenths.

Example 2: round 5,176 up to hundredths.

Rounding to an integer
If the decimal fraction needs to be rounded to an integer (up to units), we look at the number that comes immediately after the decimal point (digit – tenths). If this 5, 6, 7, 8 or 9, then to the units in the integer part we add the number 1, and discard the entire fractional part. In other cases, we simply remove the fractional part without any changes to the integer part.
Examples of rounding decimals to an integer:
- 2,15 ≈ 2;
- 4,64 ≈ 5;
- 7,063 ≈ 7;
- 12,814 ≈ 13.
Note: If a fraction needs to be rounded to an integer greater than one (tens, hundreds, thousands, etc.), discard the fractional part, then round the result according to the rules for rounding natural numbers.
Example 1: rounding up to tenths of a number 156,71:
![]()
Example 2: rounding to hundreds 8134,145:
![]()
Special case: last digit is zero
If, as a result of rounding the decimal fraction, the last digit in the fractional part remains 0, it cannot be removed. This is necessary in order to clearly understand to what digit the rounding was performed.
Examples of rounding with zero on the end
- 5,01 ≈ 5,0 (up to tenths);
- 3,199 ≈ 3,20 (up to hundredths).
Let’s take a closer look at the second example. Because the next digit after the hundredths is a digit 9, so according to the rounding rules, we add one to hundredths: 9 + 1 = 10. Therefore, we write zero in the hundredths place, and add one to the tenths (1 + 1 = 2).
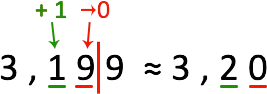










барибир чунмадим
yomon